Дипломная работа: Методические особенности изучения темы "Подобные треугольники" в средней общеобразовательной школе

k=-1-центральной симметрией.

Формулы гомотетии с центром в начале координат:

,

Если центр гомотетии имеет координаты S(x₀ , y₀ ), то формулы гомотетии с центром S имеют вид:

,

Если введем обозначения , то получим формулы

,

Основное свойство гомотетии.

Для любых точек М, N и их образов , имеет место равенство:

.

Доказательство. Воспользуемся равенствами:

, , , и найдём

.

Следствия.

1) Гомотетия с коэффициентом является преобразованием подобия с коэффициентом подобия , так как из основного свойства следует или .

2) , если k>0, и , если k<0.

3) Гомотетия плоскости обладает всеми свойствами преобразования подобия, в частности: прямую отображает в прямую, параллельные прямые - в параллельные прямые, Изменяет все расстояния в одном и том же отношении, сохраняет углы.

Характерные свойства гомотетии.

Гомотетия плоскости имеет одну неподвижную точку – центр гомотетии.

Гомотетия плоскости отображает прямую, проходящую через центр гомотетии, в себя.

Гомотетия плоскости () отображает прямую, в параллельную ей прямую, так не проходящую через центр гомотетии.

Гомотетия плоскости отображает окружность, центр которой совпадает с центром гомотетии, в концентрическую окружность. При этом радиусы окружностей связаны соотношением .

Всякие две неравные окружности гомотетичны друг другу, при этом, если окружности не являются концентрическими, существуют две гомотетии, отображающие одну из них в другую.

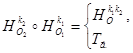
Гомотетия плоскости является преобразованием подобия первого рода.

Теорема. Всякое преобразование подобия с коэффициентом подобия k можно представить как композицию гомотетии и движения.

1.5 Группа преобразований подобия и её подгруппы

Теорема 1. Множество всех преобразований подобия плоскости есть группа преобразований, называемая группой подобий.