Дипломная работа: Методика решения иррациональных уравнений и неравенств в школьном курсе математики

Метод замены уравнения h (f (x ))=h (g (x )) уравнением f (x )=g (x ) применятся при решении иррациональных уравнений для перехода от уравнения к уравнению .

Метод введения новой переменной также разобран и на примере решения иррационального уравнения.

Отдельный пункт посвящен иррациональным неравенствам. Здесь с теоретическим обоснованием рассматривается решение неравенств вида , . В первом случае иррациональное неравенство заменяется равносильной системой неравенств 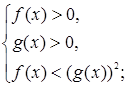во втором – равносильной совокупностью систем неравенств

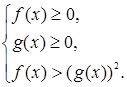
Система задач во II части данного учебного пособия изложена в той же последовательности, что и соответствующий материал в I части. В § 55 «Равносильность уравнений» изложены различные типы заданий на равносильность и следствие уравнений, в том числе и иррациональных. В § 56 «Общие методы решения уравнений» помещены задания для использования четырех методов, изложенных в I части данного учебного пособия, для решения уравнений. Все задачи в соответствии с ними разбиты на четыре блока, в каждом из которых встречаются иррациональные уравнения. В § 57 «Решение неравенств с одной переменной» изложены различные типы заданий на равносильность и следствие неравенств, в том числе и иррациональных.

В № 1673 нужно решить простейшие иррациональные уравнения. №№1674, 1675, 1712-1719 – упражнения выше среднего уровня для решения иррациональных уравнений, №№1790, 1791 – неравенств. № 1792 – упражнение повышенной трудности для решения иррациональных неравенств.

Много заданий, в которых требуется решить «смешанное» уравнение или неравенство, то есть логарифмическое, показательное или тригонометрическое уравнение или неравенство, в которое входят и иррациональные выражения. Среди этих заданий есть задания как базового, так и повышенного уровня.

В I части учебника много внимание уделено равносильности уравнений и неравенств, достаточно строго рассмотрены общие методы решения уравнений, с оговоркой о потере корней и приобретении посторонних. II часть учебника отличается обилием и разнообразием задач. Достаточно много задач на равносильность и следствие уравнений и неравенств.

1.6. «Сборник задач по алгебре, 8-9», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич [5].

Данная книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики.

В начале параграфа «Степень с рациональным показателем» помещен справочный материал теоретического характера, посвященный иррациональным уравнениям и неравенствам. Описаны такие пути решения иррациональных уравнений, как:

· возведение обеих частей уравнения в натуральную степень с последующей проверкой найденных корней;

· переход к равносильным системам, в которых учитывается область определения уравнения и требование того, что бы были неотрицательными обе части уравнения, возводимые в четную степень.

При решении иррациональных неравенств либо используется метод интервалов, либо с помощью равносильных преобразований заменяется данное иррациональное неравенство системой (или совокупностью систем) рациональных неравенств.

В параграфе рассмотрено три способа решения иррационального уравнения вида :

1) переход к равносильной системе;

2) введение новой переменной;

3) использование свойства монотонности функций.

Среди упражнений, помещенных в данном параграфе, есть упражнения для закрепления умений и навыков решать иррациональные уравнения и неравенства. В №№115-117 необходимо доказать, что уравнение не имеет решения, в №№118-119 – ответить на вопрос: равносильны ли уравнения. №№120-144 предлагаются для решения иррациональных уравнений, №№145-155 – для решения неравенств описанными выше способами.

1.7. «Алгебра и математический анализ, 11», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд [4].

Данное учебное пособие представляет собой продолжение книги «Алгебра и начала анализа» для 10 класса и предназначено как для общеобразовательной школы, так и классов и школ с углубленным изучением курса математики.

Иррациональные уравнения и неравенства изучаются в параграфе «Степенная функция. Иррациональные выражения, уравнения и неравенства» VIII главы «Показательная, логарифмическая и степенные функции».

Пункт «Иррациональные уравнения» начинается с определения иррационального уравнения и примеров таких уравнений. Далее сформулирована и доказана теорема о равносильных уравнениях, на которой основано решение иррациональных уравнений. Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе его части в степень с четным показателем, то могут появиться посторонние корни. Поэтому, чтобы не было необходимости подставлять найденные корни в данное уравнение, сформулировано еще два утверждения о равносильном переходе от уравнений вида и к системам, состоящим из уравнения и неравенства. Далее на примерах решения иррациональных уравнений демонстрируются данные равносильные переходы. Также автор рекомендует перед возведением обеих частей уравнения в некоторую степень «уединить радикал», то есть представить уравнение в виде . Далее данный метод применяется для решения иррациональных уравнений

После данного пункта помещены упражнения для закрепления умений решать иррациональные уравнения описанными выше методами – №216. В №215 необходимо доказать, что данные иррациональные уравнения не имеют решений.

В следующем пункте «Иррациональные неравенства» сформулированы приемы решения иррациональных неравенств вида и с помощью равносильного перехода к системе неравенств в первом случае и совокупности систем неравенств – во втором. Рассматривается решение иррационального неравенства вида с помощью равносильного перехода к неравенству . Решение каждого из видов неравенств демонстрируется на примерах.

После данного пункта помещены упражнения (№217) для закрепления умения решать иррациональные неравенства с помощью равносильных переходов, описанных выше.

Все утверждения, сформулированные в данном учебном пособии, изложены со строгим обоснованием. Описан полезный метод при решении иррациональных уравнений – метод «уединения радикала». Не смотря на то, что учебник не отличается обилием упражнений, предлагаемые задания разнообразны, различной степени сложности

Проведенный анализ позволяет сделать следующие выводы: