Дипломная работа: Моделі відкритої мережі

,

де - імовірності переходу.

Вирішимо отриману систему рівнянь

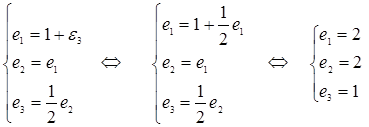
Таким чином, рівняння трафіка має єдине позитивне рішення , тобто . Позитивне в тому розумінні, що .

Розглянемо ізольований -й вузол, уважаючи, що на нього надходить найпростіший потік заявок інтенсивності (див. малюнок 1.2.1).

Малюнок 1.2.1

Він представляє із себе систему, що відрізняється від тільки тем, що інтенсивність обслуговування залежить від числа заявок у ній , .

Знайдемо стаціонарний розподіл для такого ізольованого процесу. Граф переходів зобразиться в такий спосіб.

Рівняння рівноваги для вертикальних перерізів мають вигляд ( на малюнку 1.2.2 воно зображено пунктирною лінією ).

, , ,

Тоді

.

З умови знаходимо, що

.

Таким чином, , де рівні

, (1.2.2)

, (1.2.3)

. (1.2.4)

Стаціонарний розподіл існує і єдино, якщо виконується умова ергодичності:

і (1.2.5)

Теорема 1.2.1.( Розкладання Джексона) Нехай рівняння трафіка (1.2.1) має єдине позитивне рішення й виконане умова ергодичності (1.2.5). Тоді фінальні стаціонарні ймовірності станів мережі Джексона мають вигляд

, (1.2.6)

де визначаються по формулі

, (1.2.7)