Дипломная работа: Моделі відкритої мережі

. (1.2.8)

Відповідно до теореми 1.2.1, стаціонарний розподіл представимо у формі добутку множників вузли, що характеризує; кожний множник є стаціонарний розподіл вузла, тобто

,

де з формули (1.2.2), з формули (1.2.3), з формули (1.2.4). Таким чином, стаціонарний розподіл має такий вигляд

(1.2.9)

= .

1.3 Достатня умова ергодичності

Теорема 1.3.1 (Теорема Фостера).

Регулярна Марковська ланцюг з безперервним часом і рахунковим числом станів ергодична

має нетривіальне рішення таке, що При цьому існує єдиний стаціонарний розподіл, що збігається з ергодичним. [2, с. 8-14]

Ергодичність досліджуємо відповідно до теореми 1.3.1. Розглянемо умови теореми.

Регулярність треба з того, що .

, , .

Відповідно до малюнка 1.1, одержимо:

, , .

Таким чином, регулярність виконується.

Тому що всі стани повідомляються з нульовим, тобто в будь-який стан можна перейти з нульового й у можна перейти з будь-якого стану, шляхом надходження, обслуговування й відходу заявок з мережі.

Примітка – тут ураховується, що матриця переходів неприводима.

Як нетривіальне рішення системи рівнянь із теореми 1.3.1 візьмемо . Тоді для ергодичності буде потрібно, щоб . Тоді одержимо,

,

де

,

Останній ряд сходиться по ознаці порівняння, якщо сходиться ряд

(1.3.1)

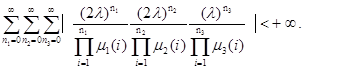
Умова (1.3.1) і є шукана умова ергодичності. Якщо ця умова буде виконаються, то буде існувати єдиний стаціонарний розподіл, що збігається з ергодичним.

2. Полумарковська модель мережі із трьома вузлами

Нехай є відкрита мережа масового обслуговування, що складає із трьох вузлів, у яку надходить найпростіший потік заявок з параметром . Причому, у першу систему масового обслуговування, що входить заявка надходить із імовірністю . Часи обслуговування заявок в -ом вузлі задані функцією розподілу часу обслуговування -им приладом однієї заявки , . При цьому накладає наступна вимога