Дипломная работа: Обучение решению задач на проценты в курсе алгебры основной школы

По-видимому, процент возник в Европе вместе с ростовщичеством. Есть мнение, что понятие процент ввел бельгийский ученый Симон Стевин. В 1584 г. он опубликовал таблицы процентов. Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.

Интересно происхождение обозначения процента. Существует версия, что знак % происходит от итальянского pro cento (сто), которое в процентных расчетах часто сокращенно писалось cto . Отсюда путем дальнейшего сокращения в скорописи буква t превратилась в наклонную черту (/), возник современный знак процента (см. схему 1).

Схема 1

Также есть предположение, что знак % возник в результате опечатки. В Париже в 1685 г. была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик напечатал знак %.

Сейчас проценты употребляются для сравнения однородных положительных количеств. Один процент – это по определению одна сотая: 1%=. Соответственно, p %= . Один процент от количества А – это, по определению, одна сотая часть количества А:

1% от А равен А .Соответственно, p % от А равен А .

Все задачи на проценты можно разделить на две основные группы.

Первая группа задач относится к той ситуации, когда даны количество А и некоторый процент p . Требуется найти количество, которое этот процент выражает.

Вопрос К1 . Каково количество, составляющее p % от А ?

Формула ответа: А .

Обсуждение решения: нужно обсудить, что принимается за базу в 100% .

Пример:

В городе N состоялись выборы в городскую думу, в которых приняли участие 75% избирателей. Только 10% от числа принявших участие в выборах отдали свои голоса партии «зеленых». Сколько жителей проголосовали за эту партию, если всего в городе 1 миллион избирателей?

Решение. Здесь нужно дважды применить формулу ответа на вопрос К1. По условию, в выборах приняли участие чел. От них 10% - это .

Ответ: 75000.

Вопрос К2 . Каково количество, p % от которого есть А ?

Формула ответа: А .

Обсуждение. Вопросы К1 и К2 родственны. Пусть искомое количество (в данном случае стопроцентная база) есть x. Тогда мы находимся в ситуации вопроса К1: А= x . Отсюда получаем формулу ответа на вопрос К2. Можно воспользоваться другим способом рассуждения при ответе на вопрос К2: если на А приходится p % , то один процент от неизвестного количества есть , соответственно неизвестное количество есть 100 .

Пример:

При помоле пшеницы получается 80% муки. Сколько пшеницы нужно смолоть, чтобы получить 480 кг пшеничной муки?

Решение:

По формуле К2 искомое количество пшеницы есть 480=600 кг

Ответ: 600 кг.

Вопрос К3 . Каково количество, большее чем А , на p % ?

Формула ответ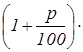а: А .

Обсуждение. В данном случае стопроцентная база – это А . Разница между неизвестным количеством и базой по условию составляет p % , что по формуле ответа на вопрос К1 дает А . В результате искомое количество есть А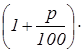+ А=А .

Вопрос К4 . Каково количество, меньшее чем А , на p % ?

Формула ответ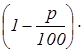а: А .

Обсуждение. Аналогично предыдущему случаю. Если ответ на данный вопрос приводит к отрицательному числу, то искомое количество считают несуществующим, а сам вопрос некорректным.