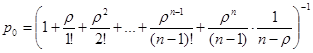
Формулы для остальных вероятностей имеют тот же вид, что и для СМО с ограниченной очередью:

Из (27) получим выражение для вероятности образования очереди заявок:

Поскольку очередь не ограничена, то вероятность отказа в обслуживании заявки:

Относительная пропускная способность:

Абсолютная пропускная способность:

Из формулы (28) при получим выражение для среднего числа заявок в очереди:

Среднее число обслуживаемых заявок определяется формулой:

Среднее время пребывания в СМО и в очереди определяется формулами (12) и (13).

5.7 Многоканальная система массового обслуживания с ограниченной очередью и ограниченным временем ожидания в очереди

Отличие такой СМО от СМО, рассмотренной в подразделе 5.5, состоит в том, что время ожидания обслуживания, когда заявка находится в очереди, считается случайной величиной, распределённой по показательному закону с параметром , где – среднее время ожидания заявки в очереди, а – имеет смысл интенсивности потока ухода заявок из очереди. Граф такой СМО изображён на рисунке 9.

Рисунок 9 – Граф многоканальной СМО с ограниченной очередью и ограниченным временем ожидания в очереди

Остальные обозначения имеют здесь тот же смысл, что и в подразделе.

Сравнение графов на рис. 3 и 9 показывает, что последняя система является частным случаем системы рождения и гибели, если в ней сделать следующие замены (левые обозначения относятся к системе рождения и гибели):

(29)

Выражения для финальных вероятностей легко найти из формул (4) и (5) с учетом (29). В результате получим:

,

где . Вероятность образования очереди определяется формулой: