Так как и правая часть исходного уравнения положительна, то . Из чего следует, что .

2) .

.

Это уравнение корней не имеет, так как .

Итак, исходное уравнение имеет единственный корень

.

Ответ: .

Алгебраическое решение

Данное уравнение легко «превратить» в рациональное уравнение восьмой степени возведением обеих частей исходного уравнения в квадрат. Поиск корней получившегося рационального уравнения затруднен, и необходимо обладать высокой степенью изобретательности, чтобы справиться с задачей. Поэтому целесообразно знать иной способ решения, менее традиционный. Например, подстановку , предложенную И. Ф. Шарыгиным [57].

Положим , тогда

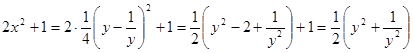
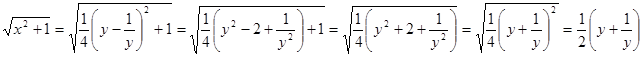Преобразуем правую часть уравнения :

.

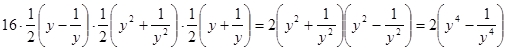С учетом преобразований уравнение примет вид

.

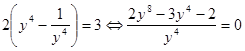Введем замену , тогда

.

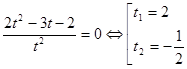Второй корень является лишним, поэтому , а .

Ответ: .

Если заранее не известна идея решения уравнения 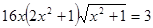, то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени 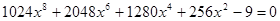, найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения 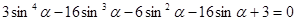, если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель – получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой 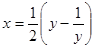технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.

Подчеркнем, что применение тригонометрической подстановки для решения задач должно быть осознанным и оправданным. Использовать подстановку целесообразно в тех случаях, когда решение другим способом сложнее или вовсе невозможно. Приведем еще один пример, который, в отличие от предыдущего, проще и быстрее решается стандартным способом.

Пример 5 . Решить уравнение

[51].

Решение с помощью тригонометрической подстановки

Так как переменная может принимать любые действительные значения, можно положить . Уравнение примет вид

.

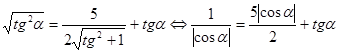В силу того, что , можно раскрыть модуль

.

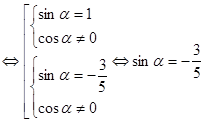Так как , то .

Ответ: .

Алгебраическое решение

Проверкой убеждаемся, что – корень.

Ответ: .

1.2 Рациональные уравнения

Тригонометрическая подстановка применяется при решении рациональных уравнений, когда уравнение не имеет рациональных корней или найденные рациональные решения не исчерпывают всего множества решений уравнения.

При решении иррациональных уравнений возможность введения тригонометрической подстановки была видна по структуре уравнения. В нескольких следующих задачах применение метода тригонометрической подстановки не так очевидно. Вот почему прежде чем ввести подстановку, нужно доказать законность такого введения.

Пример 1. Сколько корней имеет уравнение

[37].

Решение этой задачи любым методом начинается одинаково. Докажем, что все корни данного уравнения принадлежат промежутку . Действительно, если

.

Но тогда в исходном уравнении слева стоит произведение больше восьми, а справа единица, что невозможно.

Решение с помощью тригонометрической подстановки

Положим . Тогда каждому корню исходного уравнения будет соответствовать ровно один корень , где . Наоборот, каждому корню уравнения соответствует ровно один корень исходного уравнения. Таким образом, задача может быть переформулирована так: сколько корней на промежутке имеет уравнение

.

Так как и , то можно взять . Заметим, что если - корень данного уравнения, то и тоже корень. Вот почему достаточно рассмотреть , то есть отыскать только положительные решения. С учетом выше изложенного исходное уравнение перепишется в виде

.

Так как , то можно обе части равенства умножить на , получим

.

Ответ: шесть корней.

Алгебраическое решение

Так как выражение от правой части равенства четное 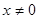и и 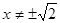, выясним вопрос о наличии корней на промежутке . Проверкой устанавливаем, что – корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции и . Так как

и функция непрерывна на числовой прямой, то найдутся такие значения и , что . Поэтому на промежутке уравнение имеет три корня, а на всей числовой прямой – шесть корней.