Дипломная работа: Расчет и анализ потерь активной мощности

, . (1.17)

Первое слагаемое (аналог обобщенного решения) характеризует близость измеренных и расчетных f(x) значений, второе слагаемое (аналог нормального решения) – близость априорных данных и решения x. Назначение параметра регуляризации – согласование меры близости в пространстве оцениваемых параметров и меры близости в пространстве наблюдений (косвенно решается проблема согласования области определения и области значений).

Решение, доставляющее минимум (1.17), называется обобщенным нормальным решением , а метод, реализующий этот критерий, – методом обобщенной нормальной оценки (МОНО) .

Параметр регуляризации обобщенно учитывает статистические свойства измерений и априорных данных, его значение задается априори как

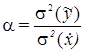
где: - дисперсия измерений; - дисперсия задания априорных данных.

При таком выборе параметра регуляризации МОНО дает неухудшающуюся, устойчивую к погрешности измерений и к изменениям параметра регуляризации оценку, а верхняя норма матрицы ковариации ошибок оценки оказывается минимальной.

В качестве априорной информации, используемой при оценке состояния реальной ЭЭС, можно использовать:

1) результаты предыдущей оценки;

2) измеренные значения напряжений (их номинальные значения); ограниченность фаз узловых напряжений (d ® 0).

Второй случай менее благоприятен. Часть априорных данных (например, измеренные напряжения) принадлежит области определения, другая часть (например, фазы узловых напряжений) может и не принадлежать к ним. Достоверность таких данных различна, полученная оценка параметра регуляризации находится в широком диапазоне (10¸10⁵ ) [2]. Целесообразно для каждой группы априорных данных ввести свои весовые коэффициенты:

а) CU₁ – для измеренных напряжений;

б) CU₂ – для номинальных напряжений (если измерений не проводилось);

в) С_d – для фаз узловых напряжений.

Тогда критерий оценки перепишется в виде

,

где: – диагональная матрица с вышеуказанными весовыми коэффициентами, – априорные данные (для фаз узловых напряжений это значения на к-ой итерации).

Для реальных ЭЭС: CU₁ =10^-2 , CU₂ =10^-4 , C_d =1, и диапазон изменения параметра регуляризации сужается: 10³ <<10⁵ [2]

1.5 Численные методы решения

Принимая во внимание все выше сказанное, в конечном счете задача оценивания состояния ЭЭС сводится к решению экстремальной задачи

(1.18)

по итерационной формуле

, (1.19)

где: k – номер итерации; – направление продвижения на (к+1) – ой итерации из точки х^к ; – коэффициент, определяющий длину шага в направлении ; – приращение на к-ой итерации; начальное приближение задается.

В результате решения (1.19) будет получена последовательность с определенными свойствами.

Для выбранной модели режима и построенного критерия оценки эффективность алгоритма оценки состояния ЭЭС определяется свойствами численного метода решения (1.19) и характеризуется такими критериями, как: скорость и надежность сходимости, точность решения, время счета, сложность алгоритма, требуемый объем оперативной памяти ЭВМ и т.д.

Численные методы решения (1.19) используют ту или иную аппроксимацию либо целевой функции

(1.20)

либо вектор-функции f(x). Наибольшее распространение получил метод Ньютона-Рафсона, в котором используется разложение в ряд Тейлора нелинейной вектор-функции f(x) в окрестности произвольной точки х^к до членов первого порядка малости включительно