Дипломная работа: Разработка бизнес-плана инвестиционного проекта на предприятии по производству компьютерных столов
Оценка потребности задает емкость рынка. Рынок не монополизирован, на рынке действуют несколько компаний-конкурентов.
Новая компания, создаваемая согласно бизнес-плану, может претендовать на какую-то долю емкости рынка. Поэтому возникает задача спрогнозировать не только общую емкость рынка (потребность), но и долю данной компании на рынке. Новая компания реально может претендовать, либо на неудовлетворенную часть спроса, либо на спрос, высвобождаемый за счет вытеснения слабых конкурентов.
Таким образом, спрос на продукцию (услугу), обеспечиваемый проектируемой компанией, определяют по формуле
, Q = 
5945 шт в год
где Qрын – емкость рынка (годовая потребность); d – доля компании на рынке, % (20%).
Прогнозирование перспективного спроса будет выполнено с помощью метода статистического моделирования – метода экстраполяции.
Экстраполяция - распространение выявленных закономерностей развития изучаемого предмета на будущее. Данный метод основан на применении математических функций.
Экстраполяция временного ряда – это проекция временного ряда на будущие периоды времени, т.е. распространение на будущее тенденций, установленных в прошлом.
Прогноз по среднему интервальному индексу изменения показателя спроса.
Показатель спроса Таблица 1.5
| Год (номер) | 1 | 2 | 3 |
| Объем продаж, шт | 27708 | 28200 | 29724 |
Индекс изменения спроса в i-м интервале в процентах:
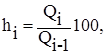
Индекс изменение спроса во 2 и 3 годах:
h2 = (28200/27708)*100 = 102%
h3 = (29724/28200)*100 = 105%
среднегодовой индекс:
hср = (105+101)/2 = 104%
Прогнозируемый спрос на 4-й год
Q = 29724*104/100 = 30913 шт
Метод простой экстраполяции. Основу метода составляет метод наименьших квадратов, результатом которого будет линейное корреляционное уравнение
y = b0 + b1*x,
где у- прогнозируемый спрос, х – номер интервала (периода).
Показатель спроса Таблица 1.6
| Годы | 2008 | 2009 | 2010 |
| Номер года, х | 1 | 2 | 3 |
| Объемы продаж, у, шт. | 27708 | 28200 | 29724 |
Расчет параметров корреляционного уравнения Таблица 1.7
| Годы | x | y | x2 | xy |
| 2008 | 1 | 27708 | 1 | 27708 |
| 2009 | 2 | 28200 | 4 | 56400 |
| 2010 | 3 | 29724 | 9 | 89172 |
| Сумма | 6 | 85632 | 14 | 173280 |
Решим систему:
14b1 + 6b0 = 173280 b0 = 26528
6b1 + 3b0 = 85632 b1 = 1008
Корреляционное уравнение прямой будет выглядеть следующим образом: y = 26528 + 1008x.
Для четвертого (2011 года): у = 26528 + 1008*4 = 30560 шт.