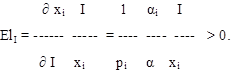Главное условие (требование) на функцию полезности – это, чтобы она отражала отношение сильного (или слабого) предпочтения в пространстве наборов, т. е. удовлетворяла условиям:

u (х) £u (у), если и только если х á у;

u (х) = u (у), если и только если х ~ у; т. е. функция полезности – неубывающая функция.

Из необходимости удовлетворять условиям 1-го закона Госсена следует, что функция полезности должна обладать 2 – мя математическими свойствами: предельная полезность i- го вида услуги положительна, т.е. частная производная ∂ u / ∂ x₁ > 0 положительна.

Для более полного использования математического аппарата от функции полезности требуют, чтобы она была 2-жды дифференцируема и матрица Гессе, состоящая из вторых частных производных, была отрицательно в любой точке.

Отметим, что аксиоматический подход к построению функций полезности обладает крупным недостатком, связанным с трудностью проверки приведенных выше предположений в реальных условиях отрасли связи. Поэтому в экономических исследованиях зачастую используются конкретные виды функций полезности, причем нужная функция подбирается, исходя из необходимости соответствия реальным фактам и наблюдениям. Работать с функцией полезности гораздо удобнее, чем с системой предпочтений.

3. Задача потребительского выбора

Задача рационального поведения потребителя на рынке товаров и услуг. Почему потребитель покупает услугу связи? Его решение базируется на 2 соображениях: а)полезности услуги связи, б)располагаемым доходом, предназначенным на оплату услуги связи.

Т. е. с начала должны быть функция полезности и будущие расходы I на все виды услуг связи. Если этих 2 "параметров" у ОДТ нет, то нет и спроса. Со стороны продавца услуги связи должна быть предъявлена цена р_i за услугу связи вида i и гарантия его предоставления. Цена служит самой важной детерминантой количества любого покупаемого продукта или услуги, но существуют и другие факторы, которые влияют на покупки услуг или продуктов.

Наша задача заключается в выборе такого набора (х₁ ⁰ ,…,х_n ⁰ ), который максимизирует его функцию полезности

при бюджетном ограничении

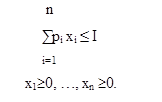
Набор (х₁ ⁰ ,…, х_n ⁰ ), который дает решение этой задачи, называется точкой локального рыночного равновесия потребителя.

Решение задачи общего вида для набора услуг

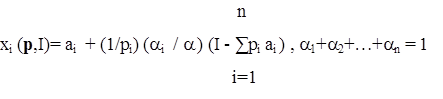
называются функциями спроса на услуги по ценам р₁ , р₂ ,…, р_n , в количествах х₁ ,…, х_n .

Заметим, что в модели учитывается суммарный бюджет I, а не ее слагаемые I₁ + I₂ +…+ I_n .

Свойства (х₁ ⁰ ,…, х_n ⁰ ):

1. Набор (х₁ ⁰ ,…, х_n ⁰ ) является решением задачи [1] для любого монотонного преобразования функции полезности u (х₁ , х₂ ).

2. Набор (х₁ ⁰ ,…, х_n ⁰ ) является решением задачи [1], если все цены и доход увеличиваются (уменьшаются) в l > 0 раз.

3. Предельная полезность i - го вида услуги положительна, т.е. частная произ водная ∂ u / ∂ x_j = α_j > 0 положительна.

Здесь а _i - минимально необходимое количество услуги, которое приобретается в любом случае и не является предметом выбора.

4. Эластичность функции спроса Р. Стоуна

Эластичность функции спроса Р. Стоуна х_i по объему i- го вида услуги а_j постоянна. Эластичность спроса — изменение спроса на данный вид услуги под влиянием экономических и социальных факторов, связанных с изменением цен на виды услуг; спрос может быть эластичным, если процентное изменение его объема (трафика) превышает снижение уровня цен, и неэластичным, если степень снижения цен выше прироста спроса.

Ценовой коэффициент эластичности всегда будет иметь отрицательный знак (т.к. закон спроса представляет собой обратную зависимость количества услуг от цены), поэтому рассматривается только абсолютная величина коэффициента эластичности.

Ценовые эластичности, зависят от знака ∂ х_j / ∂ р_j и могут быть разными, но отрицательными при I - ∑ p_i α_i > 0.

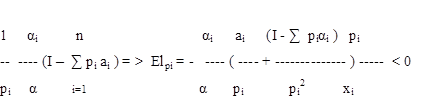
5. Свойства ценовых эластичностей

1. Эластичность спроса по цене p_i тем выше, чем выше удельный вес расходов на данный вид услуги в суммарных расходах покупателя на все присущие этому покупателю виды услуг (I - ∑ p_i α_i ) тем больше, чем больше I_i в сумме I₁ + I₂ +…+ I_n =I.

2. Эластичность спроса по цене тем выше, чем ниже субъективная необходимость в данном виде услуги. Чем ниже значение α_i , тем выше эластичность спроса по цене El_pi , т е чем меньше α_i , тем меньше по абсолютной величине El_pi , ибо El_pi <0.

3. спрос по цене считается эластичным, если ‌El_pi > 1.

6. Эластичность спроса по доходу