Дипломная работа: Структурный синтез D-элементов и лестничных arc-схем
Рассматриваемая обобщенная структура (модель) описывается векторной системой уравнений:
 (5)
(5)
Смысл векторов ![]() ,
, ![]() ,
, ![]() ,
, ![]() , Y, Z, отображающих сигналы в основных узлах схемы, поясняется на сигнальном графе, изображенном на рис. 4. Содержательная сторона других составляющих системы (5) приведена в табл. 1.
, Y, Z, отображающих сигналы в основных узлах схемы, поясняется на сигнальном графе, изображенном на рис. 4. Содержательная сторона других составляющих системы (5) приведена в табл. 1.

Рис. 4. Векторный сигнальный граф обобщенной структуры
Таблица 1
Основные составляющие обобщенной структуры
|
Матрица, вектор | Размерность |
Физический смысл компоненты матрицы (вектора) |
| Частные передачи коммутатора от источника сигнала ( | ||
| Передаточная функция ( | ||
| Передаточная функция ( | ||
| Передаточные функции j-го ОУ | ||
| Частные передачи коммутатора с выхода j-го ОУ к i-му конденсатору ( | ||
| Частные передачи коммутатора с выхода i-й RC-цепи к инвертирующему ( | ||
| Частные передачи коммутатора с выхода q-го ОУ к инвертирующему ( | ||
| Частная передача коммутатора с выхода i-й RC-цепи к нагрузке | ||
| Примечание. Здесь и далее {×} является диагональной матрицей, (×) – вектором-столбцом, [×] – вектором-строкой, I – единичной матрицей, | ||
Как видно из сигнального графа, анализируемая модель состоит из трех основных частей. Первая часть (компоненты вектора ![]() ) связывает источник сигнала
) связывает источник сигнала ![]() со входом лестничной резистивной цепи, причем
со входом лестничной резистивной цепи, причем ![]() , где ненулевая компонента соответствует номеру первого резистора резистивного эквивалента лестничной структуры.
, где ненулевая компонента соответствует номеру первого резистора резистивного эквивалента лестничной структуры.
Вторая и наиболее важная часть системы (компоненты всех матриц, входящих в (5)), осуществляет через взаимодействие базисных структур основное преобразование сигнала. Третья часть (компоненты вектора ![]() ) обеспечивает связь нагрузки с выходом базисных RC-структур.
) обеспечивает связь нагрузки с выходом базисных RC-структур.
Приведенная выше система уравнений и математические выражения (табл. 1) позволяют получить различные соотношения, характеризующие динамику ARC-устройства (передаточная функция, уравнения состояния и т.п.). Если активные элементы описываются передаточной функцией первого порядка
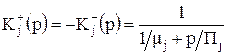 (6)
(6)
(![]() ,
, ![]() – статический коэффициент и площадь усиления ОУ), то не только передаточная функция всего устройства
– статический коэффициент и площадь усиления ОУ), то не только передаточная функция всего устройства ![]() , но и ее чувствительность
, но и ее чувствительность ![]() могут быть получены через набор локальных передаточных функций идеализированной схемы –
могут быть получены через набор локальных передаточных функций идеализированной схемы – ![]() – передаточная функция устройства при подключении источника сигнала к неинвертирующему входу j-го активного элемента,
– передаточная функция устройства при подключении источника сигнала к неинвертирующему входу j-го активного элемента, ![]() – передаточная функция устройства на его выходе,
– передаточная функция устройства на его выходе, ![]() – передаточная функция на выходе j-го активного элемента при подключении источника сигнала к его неинвертирующему входу. В этом случае
– передаточная функция на выходе j-го активного элемента при подключении источника сигнала к его неинвертирующему входу. В этом случае
 , (7)
, (7)
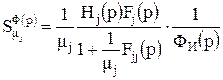 , (8)
, (8)
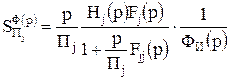 , (9)
, (9)
что, в конечном счете, и позволяет осуществить разбиение как задачи анализа, так и задачи синтеза структуры на ряд относительно самостоятельных и более простых составляющих. Решение системы (5) с учетом сказанного приводит к следующему результату
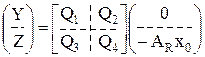 . (10)
. (10)
Так как нагрузка подключена к выходу последнего D-элемента, то
![]() , (11)
, (11)
![]() , (12)
, (12)
где вектор ![]() имеет единственную отличную от нуля компоненту, соответствующую номеру j-го ОУ.
имеет единственную отличную от нуля компоненту, соответствующую номеру j-го ОУ.
![]() , (13)
, (13)
![]() , (14)
, (14)
где вектор ![]() характеризуется аналогичной структурой.
характеризуется аналогичной структурой.
Таким образом, локальные передаточные функции ![]() , определяющие влияние аналоговых элементов на характеристики полинома, представляют собой диагональные элементы матрицы Q1.
, определяющие влияние аналоговых элементов на характеристики полинома, представляют собой диагональные элементы матрицы Q1.