Дипломная работа: Структурный синтез D-элементов и лестничных arc-схем

. (24)

Результаты анализа в соответствии с приведенными соотношениями (табл. 1), (14), (15) сведены в табл. 2 и 3. Как видно из анализа числителей локальных передаточных функций и , характер влияния площадей усиления входящих в схемы ОУ различен, что и требует более детального сопоставительного анализа схем именно по этому критерию.

Таблица 2

Структура матриц D-элемента

Схема рис.	Матрицы схем
5
6
7
8
Примечание. Для всех схем .

Таблица 3

Локальные передаточные функции D-элементов

Схема рис.	Числитель локальной передаточной функции
5
6
7
8
Примечание. Для всех схем знаменатель передаточной функции имеет вид:

Из (19) и (20) следует, что в общем случае знаменатель передаточной функции будет иметь следующий вид

. (25)

Как видно из табл. 3,

, (26)

. (27)

В соответствии с методикой [4] представим полином (25) в окрестности частоты полюса () в виде

, (28)

где

, (29)

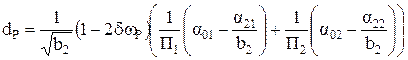. (30)

Таким образом, при реализации полного полинома второго порядка в числителе локальных функций возможна собственная компенсация влияния частоты единичного усиления на затухание полюса; что касается аналогичного влияния на частоту полюса, то это возможно, только когда воспроизводит функцию заграждающего фильтра. Результаты указанных преобразований при для рассматриваемых схем приведены в табл. 4.

Таблица 4

Погрешности реализации параметров полюса

Схема рис.	Влияние частотных свойств ОУ на параметры звеньев
5
6
7
8

Полученные результаты показывают, что потенциально более высокими частотными свойствами характеризуются звенья Антонио. Так, в случае применения идеальных ОУ в схеме рис. 5 при наблюдается взаимная компенсация влияния первого и второго ОУ на затухание полюса, а в схеме рис. 6 – собственная компенсация, которая свободна от указанного ограничения. Однако ни одна из существующих схем не обеспечивает минимизацию влияния ОУ на положение частоты полюса.

4. Динамический диапазон обобщенной структуры устойчивых D-элементов

Верхняя граница динамического диапазона любой ARC-схемы определяется не только максимальным выходным напряжением активных элементов при заданном коэффициенте нелинейных искажений, но и свойствами схемы. В общем случае на выходах активных элементов и, в частности, ОУ, в рабочем диапазоне частот W напряжения могут превышать выходное напряжение схемы (всплески коэффициента передачи – перенапряжения), определяемое входным сигналом и максимальным коэффициентом передачи , (). Именно поэтому верхний уровень динамического диапазона определяется соотношением

, () или , (), (31)

где , ().

Таким образом, в лестничных структурах, построенных на базе D-элементов, нагрузка подключается к выходу частотозависимой цепи , что в конечном итоге и уменьшает максимально возможный уровень неискаженного сигнала.

Основное влияние на динамический диапазон схемы оказывают собственные шумы, которые обусловлены шумовыми свойствами резисторов и активных элементов. При параметрической оптимизации вклад резистивных элементов можно существенно уменьшить выбором их номиналов и типов. Например, для уменьшения значений номиналов резисторов до уровня нагрузочной способности ОУ или других АЭ можно всегда увеличить емкость конденсатора. В этой связи при проектировании высококачественных схем необходимо сконцентрировать усилия на минимизации вклада активных элементов в собственный шум схемы. В этом случае

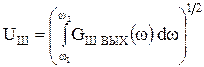, (32)

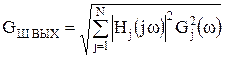, (33)

где – эквивалентная спектральная плотность мощности источников шумовой модели j-го ОУ; – границы рабочего диапазона частот W.