Дипломная работа: Теория игр
В игре, матрица которой имеет размерность m ´ n , стратегии первого игрока задаются наборами вероятностей 
(x 1 , x 2 ,..., xm ), с которыми игрок применяет свои чистые стратегии. Эти наборы можно рассмотреть как m -мерные векторы, для координат которых выполняются условия
, xi ³ 0, 
.
Аналогично для второго игрока наборы вероятностей определяют n -мерные векторы 
(y 1 , y 2 ,..., yn ), для координат которых выполняются условия
= 1, yj ³ 0, 
.
Выигрыш первого игрока при использовании смешанных стратегий определяют как математическое ожидание выигрыша, т.е. он равен
.
Теорема 1. (Неймана. Основная теорема теории игр ) Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий. Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: a£v £b. Применение первым игроком оптимальной стратегии 
опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение
, 
.
Аналогично для второго игрока оптимальная стратегия опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение
, .
Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому матрицы большой размерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и не доминирующих стратегий.
Определение 2. Дублирующими называются стратегии, у которых соответствующие элементы платежной матрицы одинаковы.
Определение 3. Если все элементы i-й строки платежной матрицы больше соответствующих элементов k-й строки, то i-я стратегия игрока А называется доминирующей над k-й стратегией. Если все элементы j-го столбца платежной матрицы меньше соответствующих элементов k-го столбца, то j-я стратегия игрока В называется доминирующей над k-й стратегией.
Пример. Рассмотрим игру, представленную платежной матрицей
.
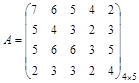a = max ( 2, 2, 3,2) = 3, b = min ( 7, 6, 6, 4,5) = 4, a ¹ b , 
.
Все элементы стратегии А 2 меньше элементов стратегии А 3 , т.е. А 2 заведомо невыгодна для первого игрока и ее можно исключить. Все элементы А 4 меньше А 3 , исключаем А 4 .
.
Для второго игрока: сравнивая В 1 и В 4 , исключаем В 1 ; сравнивая В 2 и В 4 , исключаем В 2 ; сравнивая В 3 и В 4 , исключаем В 3 . В результате преобразований получим матрицу
.
a = max ( 2,3) = 3, b = min ( 4,5) = 4, a ¹ b , .
1.4 Решение игр графическим методом
Графический метод применим к играм, в которых хотя бы один игрок имеет только две стратегии.
Первый случай. Рассмотрим игру (2 ´ 2) с матрицей
без седловой точки. Решением игры являются смешанные стратегии игроков (x 1 , x 2 ) и (y 1 , y 2 ), где x 1 - вероятность применения первым игроком первой стратегии,x 2 - вероятность применения первым игроком второй стратегии,y 1 - вероятность применения вторым игроком первой стратегии,y 2 - вероятность применения вторым игроком второй стратегии. Очевидно, что
x 1 + x 2 = 1, y 1 + y 2 = 1.
Найдем решение игры графическим методом. На оси О X отложим отрезок, длина которого равна единице. Левый конец (x = 0) соответствует стратегии первого игрока А 1 , правый (x = 1) - стратегии А 2 . Внутренние точки отрезка будут соответствовать смешанным стратегиям 
(x 1 , x 2 ) первого игрока, где x 1 =1 - x 2 . Через концы отрезка проведем прямые, перпендикулярные оси О X , на которых будем откладывать выигрыш при соответствующих чистых стратегиях. Если игрок В применяет стратегию В 1 , то выигрыш при использовании первым игроком стратегий А 1 и А 2 составит соответственно а 11 и а 21 . Отложим эти точки на прямых и соединим их отрезком В 1 В 1 . Если игрок А применяет смешанную стратегию, то выигрышу соответствует некоторая точка М , лежащая на этом отрезке. (см. рис.1)
 |
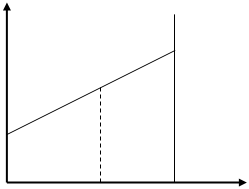В1 а21
М