Дипломная работа: Теория остатков
т.е.
r 1
r 2
= q 3 +
1
r 2 / r 3
. . . . . . .
r n -2 = r n -1 q n + r n
т.е.
r n -2
r n -1
= q n +
1
r n -1 / r n
r n -1 = r n q n +1
т.е.
r n -1
r n
= q n +1 .
Значит:
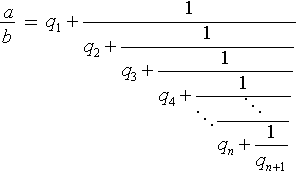
где q 1 , q 2 ,..., q n +1 - как раз те самые неполные частные из алгоритма Евклида (вот откуда название этих чисел в цепных дробях). Таким образом, в случае рационального числа a / b , процесс разложения в цепную дробь конечен и дробь содержит не более b этажей. Наиболее одаренные читатели в этом месте уже поняли, что основная теорема о цепных дробях для рациональных чисел оказалась почти доказана (не доказали только единственность разложения, но она в случае конечных цепных дробей почти очевидна - приравняйте две цепных дроби и, рассуждая по индукции, получите, что у равных дробей совпадают все неполные частные).
Пример. П ример заимствован из книги И. М. Виноградова "Основы теории чисел". Итак: разложить 105/38 в цепную дробь.
Включаем алгоритм Евклида:
105 = 38 · 2 + 29
38 = 29 · 1 + 9
29 = 9 · 3 + 2
9 = 2 · 4 + 1
2 = 1 · 2