Дипломная работа: Triple-wave ensembles in a thin cylindrical shell
Primitive nonlinear quasi-harmonic triple-wave patterns in a thin-walled cylindrical shell are investigated. This task is focused on the resonant properties of the system. The main idea is to trace the propagation of a quasi-harmonic signal — is the wave stable or not? The stability prediction is based on the iterative mathematical procedures. First, the lowest-order nonlinear approximation model is derived and tested. If the wave is unstable against small perturbations within this approximation, then the corresponding instability mechanism is fixed and classified. Otherwise, the higher-order iterations are continued up to obtaining some definite result.
The theory of thin-walled shells based on the Kirhhoff-Love hypotheses is used to obtain equations governing nonlinear oscillations in a shell. Then these equations are reduced to simplified mathematical models in the form of modulation equations describing nonlinear coupling between quasi-harmonic modes. Physically, the propagation velocity of any mechanical signal should not exceed the characteristic wave velocity inherent in the material of the plate. This restriction allows one to define three main types of elemental resonant ensembles — the triads of quasi-harmonic modes of the following kinds:
(i)high-frequency longitudinal and two low-frequency bending waves (![]() -type triads);
-type triads);
(ii)high-frequency shear and two low-frequency bending waves (![]() );
);
(iii)high-frequency bending, low-frequency bending and shear waves (![]() );
);
(iv)high-frequency bending and two low-frequency bending waves (![]() ).
).
Here subscripts identify the type of modes, namely (![]() ) — longitudinal, (
) — longitudinal, (![]() ) — bending, and (
) — bending, and (![]() ) — shear mode. The first one stands for the primary unstable high-frequency mode, the other two subscripts denote secondary low-frequency modes.
) — shear mode. The first one stands for the primary unstable high-frequency mode, the other two subscripts denote secondary low-frequency modes.
Triads of the first three kinds (i — iii) can be observed in a flat plate (as the curvature of the shell goes to zero), while the ![]() -type triads are inherent in cylindrical shells only.
-type triads are inherent in cylindrical shells only.
Notice that the known Karman-type dynamical governing equations can describe the ![]() -type triple-wave coupling only. The other triple-wave resonant ensembles,
-type triple-wave coupling only. The other triple-wave resonant ensembles, ![]() ,
, ![]() and
and ![]() , which refer to the nonlinear coupling between high-frequency shear (longitudinal) mode and low-frequency bending modes, cannot be described by this model.
, which refer to the nonlinear coupling between high-frequency shear (longitudinal) mode and low-frequency bending modes, cannot be described by this model.
Quasi-harmonic bending waves, whose group velocities do not exceed the typical propagation velocity of shear waves, are stable against small perturbations within the lowest-order nonlinear approximation analysis. However amplitude envelopes of these waves can be unstable with respect to small long-wave perturbations in the next approximation. Generally, such instability is associated with the degenerated four-wave resonant interactions. In the present paper the second-order approximation effects is reduced to consideration of the self-action phenomenon only. The corresponding mathematical model in the form of Zakharov-type equations is proposed to describe such high-order nonlinear wave patterns.
Governing equations
We consider a deformed state of a thin-walled cylindrical shell of the length ![]() , thickness
, thickness ![]() , radius
, radius ![]() , in the frame of references
, in the frame of references ![]() . The
. The ![]() -coordinate belongs to a line beginning at the center of curvature, and passing perpendicularly to the median surface of the shell, while
-coordinate belongs to a line beginning at the center of curvature, and passing perpendicularly to the median surface of the shell, while ![]() and
and ![]() are in-plane coordinates on this surface (
are in-plane coordinates on this surface (![]() ). Since the cylindrical shell is an axisymmetric elastic structure, it is convenient to pass from the actual frame of references to the cylindrical coordinates, i.e.
). Since the cylindrical shell is an axisymmetric elastic structure, it is convenient to pass from the actual frame of references to the cylindrical coordinates, i.e. ![]() , where
, where ![]() and
and ![]() . Let the vector of displacements of a material point lying on the median surface be
. Let the vector of displacements of a material point lying on the median surface be ![]() . Here
. Here ![]() ,
, ![]() and
and ![]() stand for the longitudinal, circumferential and transversal components of displacements along the coordinates
stand for the longitudinal, circumferential and transversal components of displacements along the coordinates ![]() and
and ![]() , respectively, at the time
, respectively, at the time ![]() . Then the spatial distribution of displacements reads
. Then the spatial distribution of displacements reads
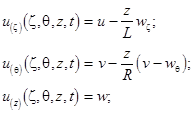
accordingly to the geometrical paradigm of the Kirhhoff-Love hypotheses. From the viewpoint of further mathematical rearrangements it is convenient to pass from the physical sought variables ![]() to the corresponding dimensionless displacements
to the corresponding dimensionless displacements ![]() . Let the radius and the length of the shell be comparable values, i.e.
. Let the radius and the length of the shell be comparable values, i.e. ![]() , while the displacements be small enough, i.e.
, while the displacements be small enough, i.e. ![]() . Then the components of the deformation tensor can be written in the form
. Then the components of the deformation tensor can be written in the form
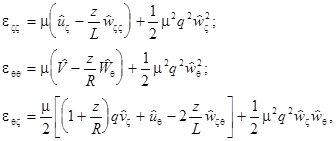
where ![]() is the small parameter;
is the small parameter; ![]() ;
; ![]() and
and ![]() . The expression for the spatial density of the potential energy of the shell can be obtained using standard stress-straight relationships accordingly to the dynamical part of the Kirhhoff-Love hypotheses:
. The expression for the spatial density of the potential energy of the shell can be obtained using standard stress-straight relationships accordingly to the dynamical part of the Kirhhoff-Love hypotheses:
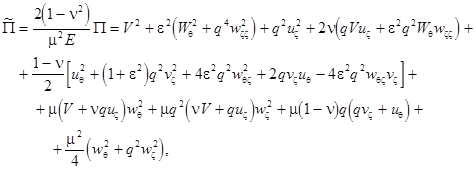
where ![]() is the Young modulus;
is the Young modulus; ![]() denotes the Poisson ratio;
denotes the Poisson ratio; ![]() (the primes indicating the dimensionless variables have been omitted). Neglecting the cross-section inertia of the shell, the density of kinetic energy reads
(the primes indicating the dimensionless variables have been omitted). Neglecting the cross-section inertia of the shell, the density of kinetic energy reads
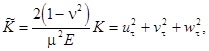
where ![]() is the dimensionless time;
is the dimensionless time; ![]() is typical propagation velocity.
is typical propagation velocity.
Let the Lagrangian of the system be ![]() .
.
By using the variational procedures of mechanics, one can obtain the following equations governing the nonlinear vibrations of the cylindrical shell (the Donnell model):
(1)
(2)
Equations (1) and (2) are supplemented by the periodicity conditions
![]()
Dispersion of linear waves
At ![]() the linear subset of eqs.(1)-(2) describes a superposition of harmonic waves
the linear subset of eqs.(1)-(2) describes a superposition of harmonic waves
(3)![]()
Here ![]() is the vector of complex-valued wave amplitudes of the longitudinal, circumferential and bending component, respectively;
is the vector of complex-valued wave amplitudes of the longitudinal, circumferential and bending component, respectively; ![]() is the phase, where
is the phase, where ![]() are the natural frequencies depending upon two integer numbers, namely
are the natural frequencies depending upon two integer numbers, namely ![]() (number of half-waves in the longitudinal direction) and
(number of half-waves in the longitudinal direction) and ![]() (number of waves in the circumferential direction). The dispersion relation defining this dependence
(number of waves in the circumferential direction). The dispersion relation defining this dependence ![]() has the form
has the form
(4)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--