Дипломная работа: Triple-wave ensembles in a thin cylindrical shell

while

where and .

Using (15) one can get the following nonlinear ordinary differential equation of the fourth order:

(16),

which describes simple stationary waves in the cylindrical shell (primes denote differentiation). Here

where and are the integration constants.

If the small parameter , and , , satisfies the dispersion relation (4), then a periodic solution to the linearized equation (16) reads

where are arbitrary constants, since .

Let the parameter be small enough, then a solution to eq.(16) can be represented in the following form

(17)

where the amplitude depends upon the slow variables , while are small nonresonant corrections. After the substitution (17) into eq.( 16) one obtains the expression of the first-order nonresonant correction

and the following modulation equation

(18),

where the nonlinearity coefficient is given by

.

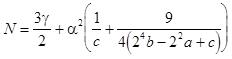Suppose that the wave vector is conserved in the nonlinear solution. Taking into account that the following relation

holds true for the stationary waves, one gets the following modulation equation instead of eq.(18):

or

,

where the point denotes differentiation on the slow temporal scale . This equation has a simple solution for spatially uniform and time-periodic waves of constant amplitude :

,

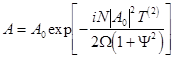which characterizes the amplitude-frequency response curve of the shell or the Stocks addition to the natural frequency of linear oscillations:

(19).