Дипломная работа: Triple-wave ensembles in a thin cylindrical shell

There are many routs to obtain the evolution equations. Let us consider a technique based on the Lagrangian variational procedure. We pass from the density of Lagrangian function to its average value

(7),

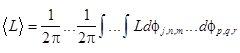An advantage of the transform (7) is that the average Lagrangian depends only upon the slowly varying complex amplitudes and their derivatives on the slow spatio-temporal scales , and . In turn, the average Lagrangian does not depend upon the fast variables.

The average Lagrangian can be formally represented as power series in :

(8)

At the average Lagrangian (8) reads

where the coefficient coincides exactly with the dispersion relation (3). This means that .

The first-order approximation average Lagrangian depends upon the slowly varying complex amplitudes and their first derivatives on the slow spatio-temporal scales , and . The corresponding evolution equations have the following form

(9)

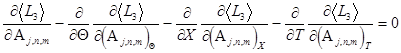
Notice that the second-order approximation evolution equations cannot be directly obtained using the formal expansion of the average Lagrangian , since some corrections of the term are necessary. These corrections are resulted from unknown additional terms of order , which should generalize the ansatz (3):

provided that the second-order approximation nonlinear effects are of interest.

Triple-wave resonant ensembles

The lowest-order nonlinear analysis predicts that eqs.(9) should describe the evolution of resonant triads in the cylindrical shell, provided the following phase matching conditions

(10),

hold true, plus the nonlinearity in eqs.(1)-(2) possesses some appropriate structure. Here is a small phase detuning of order , i.e. . The phase matching conditions (10) can be rewritten in the alternative form

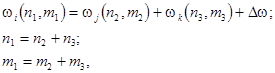
where is a small frequency detuning; and are the wave numbers of three resonantly coupled quasi-harmonic nonlinear waves in the circumferential and longitudinal directions, respectively. Then the evolution equations (9) can be reduced to the form analogous to the classical Euler equations, describing the motion of a gyro:

(11).

Here is the potential of the triple-wave coupling; are the slowly varying amplitudes of three waves at the frequencies and the wave numbers and ; are the group velocities; is the differential operator; stand for the lengths of the polarization vectors ( and ); is the nonlinearity coefficient:

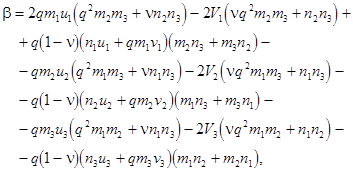
where .

Solutions to eqs.(11) describe four main types of resonant triads in the cylindrical shell, namely -, -, - and -type triads. Here subscripts identify the type of modes, namely () — longitudinal, () — bending, and () — shear mode. The first subscript stands for the primary unstable high-frequency mode, the other two subscripts denote the secondary low-frequency modes.

A new type of the nonlinear resonant wave coupling appears in the cylindrical shell, namely -type triads, unlike similar processes in bars, rings and plates. From the viewpoint of mathematical modeling, it is obvious that the Karman-type equations cannot describe the triple-wave coupling of -, - and -types, but the -type triple-wave coupling only. Since -type triads are inherent in both the Karman and Donnell models, these are of interest in the present study.

-triads

High-frequency azimuthal waves in the shell can be unstable with respect to small perturbations of low-frequency bending waves. Figure (2) depicts a projection of the corresponding resonant manifold of the shell possessing the spatial dimensions: and . The primary high-frequency azimuthal mode is characterized by the spectral parameters and (the numerical values of and are given in the captions to the figures). In the example presented the phase detuning does not exceed one percent. Notice that the phase detuning almost always approaches zero at some specially chosen ratios between and , i.e. at some special values of the parameter. Almost all the exceptions correspond, as a rule, to the long-wave processes, since in such cases the parameter cannot be small, e.g. .

NB Notice that -type triads can be observed in a thin rectilinear bar, circular ring and in a flat plate.

NBThe wave modes entering -type triads can propagate in the same spatial direction.

-triads