Дипломная работа: Triple-wave ensembles in a thin cylindrical shell
Relation (19) cannot provide information related to the modulation instability of quasi-harmonic waves. To obtain this, one should slightly modify the ansatz (17):
(20)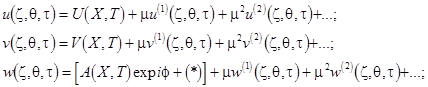
where ![]() and
and ![]() denote the long-wave slowly varying fields being the functions of arguments
denote the long-wave slowly varying fields being the functions of arguments ![]() and
and ![]() (these turn in constants in the linear theory);
(these turn in constants in the linear theory); ![]() is the amplitude of the bending wave;
is the amplitude of the bending wave; ![]() ,
, ![]() and
and ![]() are small nonresonant corrections. By substituting the expression (20) into the governing equations (1)-(2), one obtains, after some rearranging, the following modulation equations
are small nonresonant corrections. By substituting the expression (20) into the governing equations (1)-(2), one obtains, after some rearranging, the following modulation equations
(21)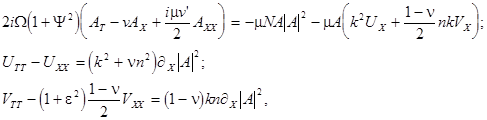
where ![]() is the group velocity, and
is the group velocity, and ![]() . Notice that eqs.(21) have a form of Zakharov-type equations.
. Notice that eqs.(21) have a form of Zakharov-type equations.
Consider the stationary quasi-harmonic bending wave packets. Let the propagation velocity be ![]() , then eqs.(21) can be reduced to the nonlinear Schrцdinger equation
, then eqs.(21) can be reduced to the nonlinear Schrцdinger equation
(22)![]() ,
,
where the nonlinearity coefficient is equal to
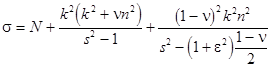 ,
,
while the non-oscillatory in-plane wave fields are defined by the following relations
![]()
and
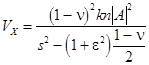 .
.
The theory of modulated waves predicts that the amplitude envelope of a wavetrain governed by eq.(22) will be unstable one provided the following Lighthill criterion
(23)![]()
is satisfied.
Envelope solitons
The experiments described in the paper [7] arise from an effort to uncover wave systems in solids which exhibit soliton behavior. The thin open-ended nickel cylindrical shell, having the dimensions ![]() cm,
cm, ![]() cm and
cm and ![]() cm, was made by an electroplating process. An acoustic beam generated by a horn driver was aimed at the shell. The elastic waves generated were flexural waves which propagated in the axial,
cm, was made by an electroplating process. An acoustic beam generated by a horn driver was aimed at the shell. The elastic waves generated were flexural waves which propagated in the axial, ![]() , and circumferential,
, and circumferential, ![]() , direction. Let
, direction. Let ![]() and
and ![]() , respectively, be the eigen numbers of the mode. The modes in which
, respectively, be the eigen numbers of the mode. The modes in which ![]() is always one and
is always one and ![]() ranges from 6 to 32 were investigated. The only modes which we failed to excite (for unknown reasons) were
ranges from 6 to 32 were investigated. The only modes which we failed to excite (for unknown reasons) were ![]() = 9,10,19. A flexural wave pulse was generated by blasting the shell with an acoustic wave train typically 15 waves long. At any given frequency the displacement would be given by a standing wave component and a traveling wave component. If the pickup transducer is placed at a node in the standing wave its response will be limited to the traveling wave whose amplitude is constant as it propagates.
= 9,10,19. A flexural wave pulse was generated by blasting the shell with an acoustic wave train typically 15 waves long. At any given frequency the displacement would be given by a standing wave component and a traveling wave component. If the pickup transducer is placed at a node in the standing wave its response will be limited to the traveling wave whose amplitude is constant as it propagates.
The wave pulse at frequency of 1120 Hz was generated. The measured speed of the clockwise pulse was 23 m/s and that of the counter-clockwise pulse was 26 m/s, which are consistent with the value calculated from the dispersion curve (6) within ten percents. The experimentally observed bending wavetrains were best fitting plots of the theoretical hyperbolic functions, which characterizes the envelope solitons. The drop in amplitude, in 105/69 times, was believed due to attenuation of the wave. The shape was independent of the initial shape of the input pulse envelope.
The agreement between the experimental data and the theoretical curve is excellent. Figure 7 displays the dependence of the nonlinearity coefficient ![]() and eigen frequencies
and eigen frequencies ![]() versus the wave number
versus the wave number ![]() of the cylindrical shell with the same geometrical dimensions as in the work [7]. Evidently, the envelope solitons in the shell should arise accordingly to the Lighthill criterion (23) in the range of wave numbers
of the cylindrical shell with the same geometrical dimensions as in the work [7]. Evidently, the envelope solitons in the shell should arise accordingly to the Lighthill criterion (23) in the range of wave numbers ![]() =6,7,..,32, as
=6,7,..,32, as ![]() .
.
REFERENCES
[1]Bretherton FP (1964), Resonant interactions between waves, J. Fluid Mech., 20, 457-472.
[2]Bloembergen K. (1965), Nonlinear optics, New York-Amsterdam.
[3]Ablowitz MJ, H Segur (1981), Solitons and the Inverse Scattering Transform, SIAM, Philadelphia.
[4]Kubenko VD, Kovalchuk PS, Krasnopolskaya TS (1984), Nonlinear interaction of flexible modes of oscillation in cylindrical shells, Kiev: Naukova dumka publisher (in Russian).
[5]Ginsberg JM (1974), Dynamic stability of transverse waves in circular cylindrical shell, Trans. ASME J. Appl. Mech., 41(1), 77-82.
[6]Bagdoev AG, Movsisyan LA (1980), Equations of modulation in nonlinear dispersive media and their application to waves in thin bodies, .Izv. AN Arm.SSR, 3, 29-40 (in Russian).
[7]Kovriguine DA, Potapov AI (1998), Nonlinear oscillations in a thin ring - I(II), Acta Mechanica, 126, 189-212.