Книга: Векторная алгебра и аналитическая геометрия

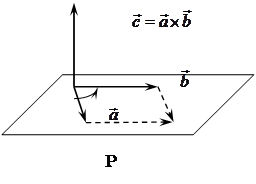
в) направлен так, что векторы , , образуют правую тройку векторов, то есть из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки (рис.2).

Координаты векторного произведения вектора на вектор определяются по формуле:

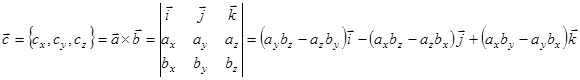
Геометрический смысл векторного произведения: модуль вектора равен площади параллелограмма, построенного на векторах и .

Свойства векторного произведения:

1) ; 2) ;

3) ; 4) и коллинеарны.

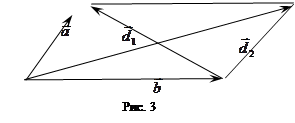?????? 3. ?????????????? ???????? ?? ???????? ? , ??? , , . ????????? ????? ?????????? ????? ???????????????, ???? ????? ??????????? ? ??????? ???????????????.

Решение.

, ,

.

Угол между диагоналями обозначим буквой , тогда

Следовательно, .

Используя свойства векторного произведения, вычислим площадь параллелограмма:

Определение. Смешанным произведением трех векторов , , называется скалярное произведение вектора на вектор :

.

Если то смешанное произведение можно вычислить по формуле:

.

Свойства смешанного произведения:

1) При перестановке любых двух векторов смешанное произведение меняет знак;

2) ; 3) ;

4) компланарны .

Геометрический смысл смешанного произведения: объем параллелепипеда, построенного на векторах , , (рис.4), а объем образованной ими треугольной пирамиды находятся по формулам .

Пример 4. Компланарны ли векторы , , ?

Решение. Если векторы компланарны, то по свойству 4) их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов, вычислив определитель:

векторы , , некомпланарны.

Деление отрезка в данном отношении.

Пусть отрезок в пространстве Oxyz задан точками и . Если он разделен точкой в отношении , то координаты точки следующие: