Книга: Векторная алгебра и аналитическая геометрия
5) Уравнения прямых ![]() и
и ![]() найдем как уравнения прямых, проходящих через две данные точки:
найдем как уравнения прямых, проходящих через две данные точки:
(![]() ):
): ![]() ,
,
(![]() ):
): ![]() (абсциссы точек
(абсциссы точек ![]() и
и ![]() одинаковые);
одинаковые);
6) Направляющим вектором высоты ![]() является нормальный вектор плоскости
является нормальный вектор плоскости ![]() . Получим уравнение плоскости
. Получим уравнение плоскости ![]() :
:
 ,
,
![]() – уравнение плоскости
– уравнение плоскости ![]() . Тогда нормальный вектор плоскости
. Тогда нормальный вектор плоскости ![]() имеет координаты
имеет координаты ![]() . Канонические уравнения прямой, проходящей через точку
. Канонические уравнения прямой, проходящей через точку ![]() параллельно вектору
параллельно вектору ![]() имеет вид:
имеет вид: ![]() ;
;
7) Для вычисления расстояния от вершины ![]() до плоскости
до плоскости ![]() воспользуемся формулой
воспользуемся формулой 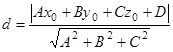 . В нашем случае
. В нашем случае ![]() – уравнение плоскости
– уравнение плоскости ![]() и
и ![]() . Итак,
. Итак,  ;
;
8) Угол ![]() между прямой
между прямой ![]() и плоскостью
и плоскостью ![]() находят по формуле:
находят по формуле:
 , где
, где ![]() – нормальный вектор плоскости
– нормальный вектор плоскости ![]() .
. ![]() и (см. п.7)
и (см. п.7) ![]() . Таким образом,
. Таким образом,  ,
,
![]() .
.
Кривые второго порядка
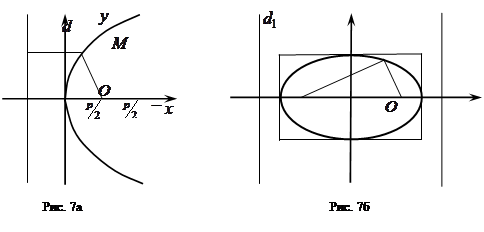
Определение. Параболой называется множество точек ![]() плоскости (см. рис.7а), для каждой из которых расстояние до данной точки
плоскости (см. рис.7а), для каждой из которых расстояние до данной точки ![]() (фокуса параболы) равно расстоянию до некоторой данной прямой
(фокуса параболы) равно расстоянию до некоторой данной прямой ![]() (директрисы). Расстояние
(директрисы). Расстояние ![]() от фокуса параболы до директрисы называется параметром параболы. Парабола – симметричная кривая; точка пересечения параболы с ее осью симметрии называется вершиной параболы.
от фокуса параболы до директрисы называется параметром параболы. Парабола – симметричная кривая; точка пересечения параболы с ее осью симметрии называется вершиной параболы.
Каноническое уравнение параболы в декартовой системе координат: ![]() .
.
Определение. Эллипс есть множество точек ![]() плоскости (см. рис.7б), для каждой из которых сумма расстояний до двух данных точек
плоскости (см. рис.7б), для каждой из которых сумма расстояний до двух данных точек ![]() и
и ![]() (фокусов) постоянна и равна
(фокусов) постоянна и равна ![]() .
.
Отрезок ![]() называется фокусным расстоянием и обозначается через
называется фокусным расстоянием и обозначается через ![]() . Середина
. Середина ![]() есть центр эллипса. Прямая, на которой лежат фокусы эллипса, называется первой осью эллипса. Прямая, проходящая через центр эллипса перпендикулярно его первой оси, называется второй осью эллипса. Оси эллипса являются его осями симметрии. Точки пересечения эллипса с осями симметрии называются его вершинами.
есть центр эллипса. Прямая, на которой лежат фокусы эллипса, называется первой осью эллипса. Прямая, проходящая через центр эллипса перпендикулярно его первой оси, называется второй осью эллипса. Оси эллипса являются его осями симметрии. Точки пересечения эллипса с осями симметрии называются его вершинами. ![]() – большая ось эллипса,
– большая ось эллипса, ![]() – малая ось.
– малая ось.
Директрисой эллипса, соответствующей данному фокусу ![]() , называется прямая
, называется прямая ![]() , перпендикулярная первой оси и отстоящая от центра эллипса на расстояние
, перпендикулярная первой оси и отстоящая от центра эллипса на расстояние ![]() , где
, где ![]() – эксцентриситет эллипса.
– эксцентриситет эллипса.
Каноническое уравнение эллипса в декартовой системе координат: ![]() , где
, где ![]() и
и ![]() – большая и малая полуоси эллипса, соответственно.
– большая и малая полуоси эллипса, соответственно.
 |
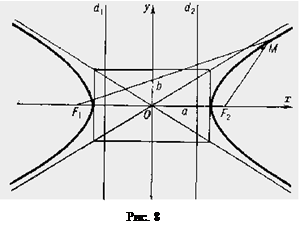
Определение. Гиперболой называется множество точек ![]() плоскости (см. рис.8) , модуль разности расстояний которых до двух данных точек
плоскости (см. рис.8) , модуль разности расстояний которых до двух данных точек ![]() и
и ![]() (фокусов гиперболы) постоянен и равен
(фокусов гиперболы) постоянен и равен ![]() . Фокусное расстояние
. Фокусное расстояние ![]() обозначают через
обозначают через ![]() . Прямая, на которой лежат фокусы, называется действительной (или фокальной осью) гиперболы. Прямая, проходящая через центр гиперболы
. Прямая, на которой лежат фокусы, называется действительной (или фокальной осью) гиперболы. Прямая, проходящая через центр гиперболы ![]() , перпендикулярно к действительной оси, называется
, перпендикулярно к действительной оси, называется
 |
?????? ????.
Директрисой гиперболы, соответствующей данному фокусу ![]() , называется прямая
, называется прямая ![]() , перпендикулярная к действительной оси, отстоящая от центра на расстояние
, перпендикулярная к действительной оси, отстоящая от центра на расстояние ![]() и лежащая от центра по одну сторону с фокусом, где
и лежащая от центра по одну сторону с фокусом, где ![]() – эксцентриситет.
– эксцентриситет.
Гипербола имеет две асимптоты, заданные уравнениями ![]() .
.
Каноническое уравнение гиперболы в декартовой системе координат: ![]() ,
,
где ![]() и
и ![]() – половины сторон основного прямоугольника гиперболы.
– половины сторон основного прямоугольника гиперболы.
Пример 9. Определить вид линии второго порядка, заданной уравнением
![]() .
.
Решение. Выделим полные квадраты по х и по у, получим:
![]() ,
,
![]() ,
,
![]() ,
,
т.е. имеем гиперболу, центр которой лежит в точке ![]() ,
, ![]() .
.
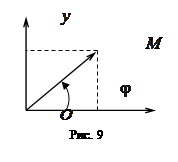 |
???????? ??????????. ??? ?????
Декартовые и полярные координаты связаны следующими соотношениями: