Книга: Векторная алгебра и аналитическая геометрия

Пример 5. Найти точку , делящую отрезок в отношении , если .

Решение. Определим координаты точки :

. Таким образом, .

Аналитическая геометрия.

Уравнение плоскости. Общее уравнение плоскости имеет вид: , , где – нормальный вектор плоскости (т.е. перпендикулярный плоскости), а коэффициент пропорционален расстоянию от начала координат до плоскости.

Уравнение плоскости, проходящей через точку перпендикулярно вектору , имеет вид

.

Уравнение плоскости, проходящей через три заданные точки , и имеет вид:

.

Угол между двумя плоскостями, имеющими нормальные векторы и , определяется как угол между векторами и по формуле:

.

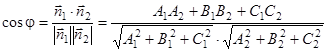Расстояние от точки до плоскости вычисляется по формуле .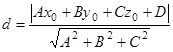

Пример 6. Написать уравнение плоскости, проходящей через точки , , .

Решение. Воспользуемся уравнением плоскости, проходящей через три заданные точки. Вычислим определитель

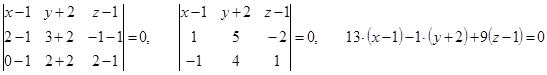, или – искомое уравнение плоскости.

Уравнение прямой на плоскости. Общее уравнение прямой на плоскости имеет вид: , где – нормальный вектор прямой (перпендикулярный прямой), а коэффициент пропорционален расстоянию от начала координат до прямой.

Уравнение прямой, проходящей через данную точку , имеет вид

или .

В другом виде , где – тангенс угла, образованного прямой и положительным направлением оси Ox, называемый угловым коэффициентом, b – ордината точки пересечения прямой с осью Oy.

Уравнение прямой, проходящей через две заданные точки и , имеет вид

.

Угол между двумя прямыми и определяется формулой

.

Расстояние от точки до прямой находится по формуле

.

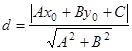Пример 7. Даны уравнения двух сторон прямоугольника , и уравнение его диагонали . Составить уравнения

????????? ?????? ? ?????? ????????? ????? ??????????????.

Решение. Сделаем схематический чертеж (Рис.6). Перепишем данные уравнения в виде: , , . Так как угловые коэффициенты прямых, задающих стороны прямоугольника, одинаковы , то эти уравнения задают параллельные прямые, то есть стороны, на них лежащие, противоположны. Найдем точки пересечения данной диагонали с этими сторонами. Пусть это будут точки и . Для этого приравняем сначала 1 и 3, а затем 2 и 3 уравнения:

; . Таким образом, .

Неизвестные стороны параллельны между собой и перпендикулярны данным (так как это прямоугольник).