Книга: Векторная алгебра и аналитическая геометрия

Таким образом, уравнения неизвестных сторон прямоугольника таковы:

. Подставив в первое уравнение координаты точки , во второе – точки , получим, что и, следовательно, , .

Найдем координаты точек и , приравняв уравнения соответствующих сторон:

, то есть ;

, то есть .

Уравнение диагонали получим как уравнение прямой, проходящей через две заданные точки и :

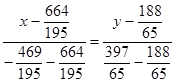или .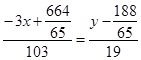

Уравнения прямой в пространстве. Прямая в пространстве Oxyz определяется как линия пересечения двух плоскостей (общие уравнения прямой в пространстве).

Канонические уравнения прямой в пространстве имеют вид

,

где – точка, через которую проходит прямая, а вектор , параллельный данной прямой, называется направляющим вектором прямой.

Уравнения прямой в пространстве, проходящей через две заданные точки и имеют вид

.

Угол между двумя прямыми с направляющими векторами и определяется по формуле

.

Пример 8. Пирамида задана координатами своих вершин , , . Требуется найти:

1) длины ребер и ; 2) угол между ребрами и ; 3) площадь грани, содержащей вершины ; 4) объем пирамиды; 5) уравнения прямых и ;

6) уравнение высоты , опущенной из вершины на плоскость ;

7) расстояние от вершины до плоскости ; 8) угол между ребром и гранью, содержащей вершины .

Решение.1) Длины ребер и определим как модуль векторов и по формулам ;

;

2) Найдем координаты векторов и :

Длины этих векторов, т.е. длины ребер и , таковы: ,

. Косинус угла между ребрами и вычислим по формуле ;

3) Площадь грани (треугольника) равна половине площади параллелограмма, построенного на векторах и , т.е. половина модуля векторного произведения этих векторов, которое равно

.

Тогда, (кв. ед);

4) Объем пирамиды равен .