Контрольная работа: Алгебра логіки як розділ математики

2. Перемикальні схеми

У комп'ютерах і інших автоматичних пристроях широко застосовуються електричні схеми, що містять сотні і тисячі перемикальних елементів: реле, вимикачів і т.п. Розробка таких схем досить трудомістка справа. Виявилося, що тут з успіхом може бути використаний апарат алгебри логіки.

Перемикальна схема - це схематичне зображення деякого пристрою, що складає з перемикачів і з'єднуючих провідників, а також із входів і виходів, на які подається і з яких знімається електричний сигнал.

Кожен перемикач має тільки два стани: замкнутий і розімкнутий. Перемикачеві Х поставимо у відповідність логічну перемінну х, що приймає значення 1 у тому і тільки в тому випадку, коли перемикач Х замкнути і схема проводить струм; якщо ж перемикач розімкнути, то х дорівнює нулеві.

Усій перемикальній схемі також можна поставити у відповідність логічну змінну, рівну одиниці, якщо схема проводить струм, і рівну нулеві - якщо не проводить. Ця змінна є функцією від змінних, відповідних усім перемикачам схеми, і називається функцією провідності.

Дві схеми називаються рівносильними, якщо через одну з них проходить струм тоді і тільки тоді, коли він проходить через іншу (при тому самому вхідному сигналі).

З двох рівносильних схем більш простою вважається та схема, функція провідності якої містить менше число логічних операцій або перемикачів.

При розгляді перемикальних схем виникають дві основні задачі: синтез і аналіз схеми.

СИНТЕЗ СХЕМИ по заданих умовах її роботи зводиться до наступних трьох етапів:

· складанню функції провідності по таблиці істинності, що відбиває ці умови;

· спрощенню цієї функції;

· побудові відповідної схеми.

АНАЛІЗ СХЕМИ зводиться до

· визначенню значень її функції провідності при всіх можливих наборах вхідних у цю функцію перемінних.

· одержанню спрощеної формули.

Приклади.

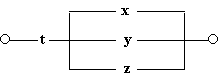
1. Побудуємо схему, що містить 4 перемикачі x, y, z і t, таку, щоб вона проводила струм тоді і тільки тоді, коли замкнути контакт перемикача t і який-небудь з інших трьох контактів.

Рішення. У цьому випадку можна обійтися без побудови таблиці істинності. Очевидно, що функція провідності має вигляд F (x, y, z, t) = t · (x v y v z), а схема виглядає так:

Приклад 2. Проаналізувати задану схему

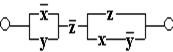
Розв’язок

В даному випадку будувати таблицю істинності не потрібно.

Приклад 3

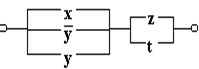
Розв’язок