Контрольная работа: Алгебра логіки як розділ математики
Теоретичні відомості.
1. Алгебра логіки
Алгебра логіки - це розділ математики, що вивчає висловлення, розглянуті з точки зору їхніх логічних значень (істинності або хибності) і логічних операцій над ними.
Логічне висловлення - це будь-яка оповідальне речення, у відношенні якого можна однозначно сказати, істинне воно або хибне. Щоб звертатися до логічних висловлень, їм призначають імена.
Операції над логічними висловленнями:
НЕ Операція, що виражається словом "не", називається запереченням і позначається рискою над висловленням (або знаком). Висловлення істинне, коли A хибне, і хибне, коли A істинне.
І Операція, що виражається зв'язуванням "і", називається кон’юнкцією (лат. conjunctio - з'єднання) або логічним множенням і позначається точкою " " (може також позначатися знаками або &). Висловлення А·В істинно тоді і тільки тоді, коли обидва висловлення А и В істинні.
АБО Операція, що виражається зв'язуванням "або" (у невиключаючому сенсі) називається диз'юнкцією (лат. disjunctio - поділ) або логічним додаванням і позначається знаком v (або плюсом). Висловлення А v В помилкове тоді і тільки тоді, коли обидва висловлення А и В помилкові.
ЯКЩО-ТО Операція, що виражається зв'язуваннями "якщо., то", "з. випливає",". витікає.", називається імплікацією (лат. implico - тісно зв'язані) і позначається знаком. Висловлення помилкове тоді і тільки тоді, коли А істинно, а В хибне.
РІВНОСИЛЬНА Операція, що виражається зв'язуваннями "тоді і тільки тоді", "необхідно і досить",". рівносильно.", називається еквіваленцією або подвійною імплікацією і позначається знаком або ~. Висловлення істинне тоді і тільки тоді, коли значення А и В збігаються. За допомогою логічних змінних і символів логічних операцій будь-яке висловлення можна формалізувати, тобто замінити логічною формулою. В алгебрі логіки виконуються наступні основні закони, що дозволяють робити тотожні перетворення логічних виражень:
Рівносильні перетворення логічних формул мають те ж призначення, що і перетворення формул у звичайній алгебрі. Вони служать для спрощення формул або приведення їх до визначеного виду шляхом використання основних законів алгебри логіки. Під спрощенням формули, що не містить операцій імплікації і еквіваленції, розуміють рівносильне перетворення, що приводить до формули, що або містить у порівнянні з вихідною менше число операцій кон’юнкції і диз'юнкції і не містить заперечень неелементарних формул, або містить менше число входжень змінних.
| Закон | Для АБО | Для І |
| Комутативний | ||
| Асоціативний | ||
| Дистрибутивний | ||
| Правила де Моргана | ||
| Тавтології | ||
| Поглинання | ||
| Склеювання | ||
| Операція над змінною з її інверсією | ||
| Правила операцій з константами | ||
| Закон подвійного заперечення |
Приклади
1.
![]()
2.
![]()
3.
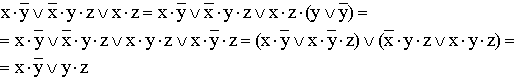
4.
![]()
5.
![]()
6.
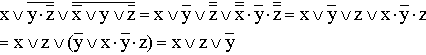
7.
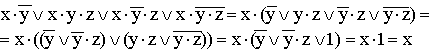
8.
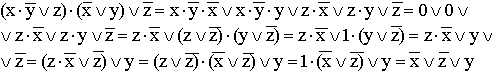
9.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--