Контрольная работа: Чисельне розвязання задач оптимального керування

, (22)

. (23)

Границя в (23) існує, якщо : або .

Самостійний інтерес становить задача з експоненціальною функцією витрат

,

,

де .

Для розв’язання багатоетапних задач оптимального стохастичного керування з мультиплікативним функціоналом витрат використовується таке рекурентне співвідношення алгоритму динамічного програмування:

, ,

де – щільність розподілу величини .

5. Мінімаксне керування

Розглянемо задачу керування системою, у якій некерованими впливами є стратегії супротивника (або явища природи) , , що обираються залежно від поточного стану і керування . Вважатимемо, що припустимі стратегії супротивника приймають значення із множини , . Будемо обчислювати стратегію керування , орієнтуючись на найгіршу поведінку супротивника. Розглянемо відображення , задане формулою

,

за таких припущень:

параметр приймає значення з деякої множини , а – непуста підмножина при будь-яких , ;

функції і відображують множину в множини та відповідно, тобто , ;

скаляр додатний.

За таких умов припущення про монотонність для відображення має місце. Якщо при цьому , і для всіх , , , то відповідну -крокову задачу мінімаксного керування можна сформулювати так:

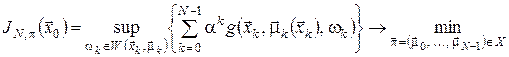, (17)

. (18)

Задача з нескінченним горизонтом формулюється аналогічно:

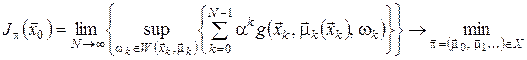, (24)

. (25)

Границя у співвідношенні (25) існує при виконанні будь-якої з умов:

· , , , ;

· , , , ;

· , , , , і деякого .

Для розв’язання багатокрокових мінімаксних задач оптимального стохастичного керування рекурентне співвідношення алгоритму динамічного програмування використовується у такому вигляді:

, ,