Контрольная работа: Движение тел

Одинаковые по величине заряды q₁ , q₂ и q₃ находятся в трех вершинах квадрата. Как направлена сила, действующая на заряд q₂ со стороны двух других зарядов? Ответ обосновать.

РЕШЕНИЕ:

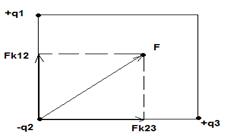
Из закона Кулона следует, что разноименные заряды притягиваются. Следовательно F_{R 1,2} , действующая со стороны первого заряда на второй заряд, направлена по линии, соединяющей эти два заряда от второго к первому. Аналогично и сила F_{R 2,3} направлена от второго к третьему. Так как заряды q1=q3 и расстояния Sq1q2=Sq2q3,

то по закону Кулона следует, что F_{R 1,2} по модулю равна F_{R 2,3}

Используя принцип суперпозиции сил проведем векторное сложение F_{R 1,2} и F_{R 2,3}

F= F_{R 1,2} + F_{R 2,3}

Таким образом, сила F будет направлена по диагонали квадрата, как показано на рисунке.

7. Незаряженное металлическое тело М, смотри рисунок, внесли в электрическое поле положительного заряда , а затем разделили на две части и . Каким зарядом обладают части тела и после их разделения?

РЕШЕНИЕ:

После внесения незаряженного металлического тела М в электрическое поле положительного заряда q, в зону I согласно закону Кулона начнут притягиваться свободные отрицательно заряженные частицы тела М (электроны), а в зону II – положительно заряженные частицы (условно «дырки»). Таким образом после разделения тела М в его I части скопится отрицательный заряд, равный по модулю положительному заряду, скопившемуся в части II.

8. Электростатическое поле создается равномерно заряженной бесконечной плоскостью. Покажите, что это поле является однородным.

РЕШЕНИЕ:

Пусть поверхностная плотность заряда равна s. Очевидно что вектор Е может быть только перпендикулярным заряженной плоскости. Кроме того очевидно, что в симметричных относительно этой плоскости точках вектор Е одинаков по модулю и противоположен по направлению. Такая конфигурация поля подсказывает, что в качестве замкнутой поверхности следует выбрать прямой цилиндр, где предполагается что s больше нуля. Поток сквозь боковую поверхность этого цилиндра равен нулю, и поэтому полный поток через всю поверхность цилиндра будет равным 2*Е*DS, где DS – площадь каждого торца. Согласно теореме Гаусса

2*Е*DS=s*DS,

где s*DS – заряд заключенный внутри цилиндра.

Откуда

Е=s/2*Ео.

Точнее это выражение следует записать так:

Еn=s/2*Eo,

где Еn – проекция вектора Е на нормаль n к заряженной плоскости, причем вектор n направлен от этой плоскости.

Тот факт, что Е не зависит от расстояния до плоскости, означает, что соответствующее электрическое поле является однородным.

9. Из медной проволоки изготовлена четверть окружности радиусом 56 см. По проволоке равномерно распределен заряд с линейной плотностью 0,36 нКл/м. Найдите потенциал в центре окружности.

РЕШЕНИЕ:

Так как заряд линейно распределен по проволоке для нахождения потенциала в центре воспользуемся формулой:

Где s - линейная плотность заряда, dL – элемент проволоки.

10. В электрическом поле, созданном точечным зарядом Q, по силовой линии из точки расположенной на расстоянии r₁ от заряда Q в точку, расположенную на расстоянии r₂ , перемещается отрицательный заряд -q. Найдите приращение потенциальной энергии заряда -q на этом перемещении.

РЕШЕНИЕ: