Контрольная работа: Движение тел
Так как круговой виток с током находится в однородном магнитном поле, на него действует сила Ампера. В соответствии с формулой dF=I[dL,B] результирующая амперова сила, действующая на виток с током определяется:
Где интегрирование проводится по данному контуру с током I. Так как магнитное поле однородно, то вектор В можно вынести из-под интеграла и задача сволится к вычислению векторного интеграла 
. Этот интеграл представляет замкнутую цепочку элементарных векторов dL, поэтому он равен нулю. Значит и F=0, то есть результирующая амперова сила равна нулю в однородном магнитном поле.
13. По короткой катушке, содержащей 90 витков диаметром 3 см, идет ток. Напряженность магнитного поля, созданного током на оси катушки на расстоянии 3 см от нее равна 40 А/м. Определите силу тока в катушке.
РЕШЕНИЕ:
Считая, что магнитная индукция в точке А есть суперпозиция магнитных индукций, создаваемых каждым витком катушки в отдельности:
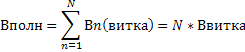
Для нахождения Ввитка воспользуемся законом Био-Савара-Лапласа.
Где, dBвитка – магнитная индукция поля, создаваемая элементом тока IDL в точке, определяемой радиус-вектором r Выделим на конце элемент dL и от него в точку А проведем радиус-вектор r. Вектор dBвитка направим в соответствие с правилом буравчика.
Согласно принципу суперпозиции:
Где интегрирование ведется по всем элементам dLвитка. Разложим dBвитка на две составляющие dBвитка(II) – параллельную плоскости кольца и dBвитка(I) – перпендикулярную плоскости кольца. Тогда
Заметив, что 
из соображений симметрии и что векторы dBвитка(I) сонаправленные, заменим векторное интегрирование скалярным:
Где dBвитка(I) =dBвитка*cosb и
Поскольку dl перпендикулярен r
Сократим на 2p и заменим cosb на R/r1
Выразим отсюда I зная что R=D/2
согласно формуле связывающей магнитную индукцию и напряженность магнитного поля:
В=Мо*Н,
тогда по теореме Пифагора из чертежа:
14. В однородное магнитное поле в направлении перпендикулярном силовым линиям влетает электрон со скоростью 10۰106 м/с и движется по дуге окружности радиусом 2,1 см. Найдите индукцию магнитного поля.
РЕШЕНИЕ: