Контрольная работа: Двоїста задача лінійного програмування: економічна інтерпретація знаходження оптимальних планів
Розглянемо тепер цю саму задачу з іншого погляду. Допустимо, що за певних умов доцільно продавати деяку частину чи всі наявні ресурси. Необхідно визначити ціни ресурсів. Кожному ресурсу ![]() поставимо у відповідність його оцінку
поставимо у відповідність його оцінку ![]() . Умовно вважатимемо, що
. Умовно вважатимемо, що ![]() – ціна одиниці і- го ресурсу.
– ціна одиниці і- го ресурсу.
На виготовлення одиниці j- го виду продукції витрачається згідно з моделлю (3.1) – (3.3) m видів ресурсів у кількості відповідно ![]() . Оскільки ціна одиниці і- го виду ресурсу дорівнює
. Оскільки ціна одиниці і- го виду ресурсу дорівнює ![]() , то загальна вартість ресурсів, що витрачаються на виробництво одиниці j- го виду продукції, обчислюється у такий спосіб:
, то загальна вартість ресурсів, що витрачаються на виробництво одиниці j- го виду продукції, обчислюється у такий спосіб:
![]() .
.
Продавати ресурси доцільно лише за умови, що виручка, отримана від продажу ресурсів, перевищує суму, яку можна було б отримати від реалізації продукції, виготовленої з тих самих обсягів ресурсів, тобто:
![]() .
.
Зрозуміло, що покупці ресурсів прагнуть здійснити операцію якнайдешевше, отже, необхідно визначити мінімальні ціни одиниць кожного виду ресурсів, за яких їх продаж є доцільнішим, ніж виготовлення продукції. Загальну вартість ресурсів можна виразити формулою:
![]() .
.
Отже, в результаті маємо двоїсту задачу :
![]() (3.4)
(3.4)
за умов: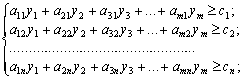 (3.5)
(3.5)
![]() (3.6)
(3.6)
Тобто необхідно визначити, які мінімальні ціни можна встановити для одиниці кожного і- го виду ресурсу ![]() , щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
, щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
Зауважимо, що справжній зміст величин ![]() – умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadowprices» у літературі перекладають як «оцінка» або «тіньова, неявна ціна». Академік Л.В. Канторович назвав їх об’єктивно обумовленими оцінками відповідного ресурсу.
– умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadowprices» у літературі перекладають як «оцінка» або «тіньова, неявна ціна». Академік Л.В. Канторович назвав їх об’єктивно обумовленими оцінками відповідного ресурсу.
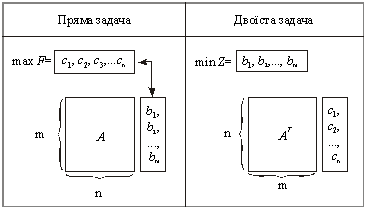
Задача (3.4) – (3.6) є двоїстою або спряженою до задачі (3.1) – (3.3), яку називають прямою (основною, початковою). Поняття двоїстості є взаємним. По суті мова йде про одну і ту ж задачу, але з різних поглядів. Дійсно, не важко переконатися, що двоїста задача до (3.4) – (3.6) збігається з початковою. Тому кожну з них можна вважати прямою, а іншу – двоїстою. Симетричність двох таких задач очевидна. Як у прямій, так і у двоїстій задачі використовують один набір початкових даних: ![]() ,
, ![]() ;
; ![]() . Крім того, вектор обмежень початкової задачі стає вектором коефіцієнтів цільової функції двоїстої задачі і навпаки, а рядки матриці А (матриці коефіцієнтів при змінних з обмежень прямої задачі) стають стовпцями матриці коефіцієнтів при змінних в обмеженнях двоїстої задачі. Кожному обмеженню початкової задачі відповідає змінна двоїстої і навпаки.
. Крім того, вектор обмежень початкової задачі стає вектором коефіцієнтів цільової функції двоїстої задачі і навпаки, а рядки матриці А (матриці коефіцієнтів при змінних з обмежень прямої задачі) стають стовпцями матриці коефіцієнтів при змінних в обмеженнях двоїстої задачі. Кожному обмеженню початкової задачі відповідає змінна двоїстої і навпаки.
Початкова постановка задачі та математична модель може мати вигляд як (3.1) – (3.3), так і (3.4) – (3.6). Отже, як правило, кажуть про пару спряжених задач лінійного програмування.
2.1 Правила побудови двоїстих задач
Для побудови двоїстої задачі необхідно звести пряму задачу до стандартного виду. Вважають, що задача лінійного програмування подана у стандартному вигляді, якщо для відшукання максимального значення цільової функції всі нерівності її системи обмежень приведені до виду «![]() », а для задачі на відшукання мінімального значення – до виду «
», а для задачі на відшукання мінімального значення – до виду «![]() ».
».
Якщо пряма задача лінійного програмування подана в стандартному вигляді, то двоїста задача утворюється за такими правилами :
1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.
2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі.
3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі – на визначення найменшого значення (min), і навпаки.
4. Коефіцієнтами при змінних у цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.
5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних у цільовій функції прямої задачі.
6. Матриця
 ,
,
що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двоїстої задачі
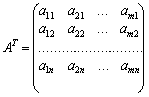
утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків – рядками.
Процес побудови двоїстої задачі зручно зобразити схематично: