Контрольная работа: Двоїста задача лінійного програмування: економічна інтерпретація знаходження оптимальних планів

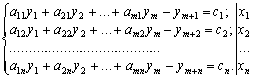
Отримали таку відповідність між змінними спряжених задач:

Наступна теорема в літературі, як правило, має назву теореми про доповнюючу нежорсткість.

Теорема (друга теорема двоїстості для симетричних задач ). Для того, щоб плани X* та Y* відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:

(3.22)

. (3.23)

Доведення. Необхідність . Нехай X* та Y* – оптимальні плани відповідно прямої та двоїстої задач (3.20) i (3.21). З першої теореми двоїстості відомо, що

,

а також компоненти векторів X* та Y* задовольняють системи обмежень задач (3.20) та (3.21), тобто:

, (3.24)

. (3.25)

Помножимо (3.24) на , а (3.25) – на і підсумуємо праві та ліві частини. Отримаємо:

;

Праві частини останніх двох нерівностей не збігаються, але оскільки їх ліві частини однакові, то це означає, що разом вони виконуються лише за умови рівностей, тобто:

;

Виконаємо перетворення для кожного рівняння:

; (3.26)

. (3.27)

Оскільки , то в рівнянні (3.26) кожна з компонент , а , тому виконання рівняння (3.26) можливе лише у тому разі, коли кожний доданок виду . Аналогічне міркування проведемо для (3.27), після чого можна висновувати, що .

Достатність . За умовою виконуються рівняння

,

, .

Необхідно довести, що X* та Y* – оптимальні плани відповідно прямої (3.20) та двоїстої (3.21) задач. У кожному рівнянні розкриємо дужки та підсумуємо перше рівняння по , а друге – по . Отримаємо:

;

.

Ліві частини цих рівнянь однакові, отже, . Тоді за першою теоремою двоїстості, оскільки значення цільових функцій цих задач збігаються, можна висновувати, що X* та Y* – оптимальні плани спряжених симетричних задач. Теорему доведено.

Очевидніший взаємозв’язок між оптимальними планами прямої та двоїстої задач встановлює наслідок другої теореми двоїстості.