Контрольная работа: Двоїста задача лінійного програмування: економічна інтерпретація знаходження оптимальних планів

,

тобто всі компоненти вектора є оцінками оптимального плану задачі (3.1) – (3.3), а тому

. (3.16)

Оскільки оптимальний план початкової задачі подано у вигляді , то за правилами побудови двоїстої задачі можна допустити, що її оптимальний план матиме вигляд:

. (3.17)

Доведемо, що дійсно є оптимальним планом двоїстої задачі.

Система обмежень двоїстої задачі у векторно-матричній формі матиме вигляд: .

Підставимо в цю нерівність значення . Тоді, враховуючи (3.15), (3.16) та (3.17), отримаємо: .

Звідки: . Отже, задовольняє систему обмежень (3.5) двоїстої задачі, тому є допустимим планом задачі (3.4) – (3.6).

Для даного плану значення функціонала дорівнюватиме:

, (3.18)

де . Підставимо в (3.18) значення з (3.17) та, враховуючи (3.13), матимемо:

. (3.19)

Доведено, що збігається зі значенням оптимального плану початкової задачі.

Отже, за лемою 3.2 (достатня умова оптимальності плану задачі лінійного програмування) план є оптимальним планом двоїстої задачі (3.4) – (3.6).

Аналогічно доводиться, що коли двоїста задача має розв’язок, то початкова також має розв’язок і виконується рівність: .

Для доведення другої частини теореми допустимо, що лінійна функція початкової задачі необмежена зверху. Тоді з нерівності маємо, що , що не має змісту. Отже, двоїста задача в даному разі не має розв’язків. Доведена теорема дає змогу в процесі розв’язування однієї задачі водночас знаходити план другої.

Економічний зміст першої теореми двоїстості . Максимальний прибуток (Fmax) підприємство отримує за умови виробництва продукції згідно з оптимальним планом , однак таку саму суму грошей () воно може мати, реалізувавши ресурси за оптимальними цінами . За умов використання інших планів на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво.

3.2 Друга теорема двоїстості

Між розв’язками спряжених задач крім рівності значень цільових функцій існує тісніший взаємозв’язок. Для його дослідження розглянемо дві симетричні задачі лінійного програмування.

Пряма задача:

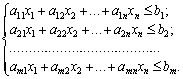(3.20)

.

Двоїста задача:

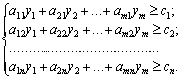(3.21)

Для розв’язування задач симплексним методом необхідно звести їх доканонічної форми, для чого в системи обмежень задач (3.20) і (3.21) необхідно ввести відповідно m та n невід’ємних змінних. Поставимо обмеженням кожної задачі у відповідність змінні її двоїстої задачі.