Контрольная работа: Економіко-математичне програмування

Завдання 1

Побудувати математичну модель задачі.

На підприємстві виготовляються вироби двох видів А і В. Для цього використовується сировина чотирьох типів – І, ІІ, ІІІ, ІV, запаси якої дорівнюють, відповідно, 21; 4; 6; 10 од. Для виготовлення одного виробу А необхідна така кількість одиниць сировини чотирьох видів: 2; 1; 0; 2. Для виробу В – 3; 0; 1; 1 од. відповідно. Випуск одного виробу А дає 3 грн. од. прибутку, типу В – 2 грн. од. Скласти план виробництва, який забезпечує найбільший прибуток.

Сировина	Норма витрат сировини, од		Запаси сировини, од.
	А	В
І	2	3	21
ІІ	1	0	4
ІІІ	0	1	6
ІV	2	1	10
Ціна, грн. од.	3	2

Розв’язок

Складаємо математичну модель задачі. Позначимо через х ₁ кількість виробів 1-ї моделі, що виготовляє підприємство за деяким планом, а через х₂ кількість виробів 2-ї моделі. Тоді прибуток, отриманий підприємством від реалізації цих виробів, складає

∫ = 3х₁ +2х₂ .

Витрати сировини на виготовлення такої кількості виробів складають відповідно:

C_I =2х₁ + 3х₂ ,

C_II =1х₁ + 0х₂ ,

C_III =0х₁ + 1х₂ ,

C_IV =2х₁ + 1х₂ ,

Оскільки запаси сировини обмежені, то повинні виконуватись нерівності:

2х₁ + 3х₂ ≤ 21

1х₁ ≤ 4

1х₂ ≤ 6

2х₁ + 1х₂ ≤ 10

Оскільки, кількість виробів є величина невід'ємна, то додатково повинні виконуватись ще нерівності: х₁ > 0, х₂ > 0.

Таким чином, приходимо до математичної моделі (задачі лінійного програмування):

Знайти х₁ , х₂ такі, що функція ∫ = 3х₁ +2х₂ досягає максимуму при системі обмежень:

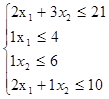
Розв'язуємо задачу лінійного програмування симплексним методом.

Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних. Оскільки маємо змішані умови-обмеження, то введемо штучні змінні x.

2x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ = 21

1x₁ + 0x₂ + 0x₃ + 0x₄ + 0x₅ + 1x₆ = 4

0x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 6

2x₁ + 1x₂ + 0x₃ + 0x₄ + 1x₅ + 0x₆ = 10

де х₁ ,...,х₆ >0

Для постановки задачі на максимум цільову функцію запишемо так:

F(X) = 3 x₁ +2 x₂ - M x₆ =>max

--> ЧИТАТЬ ПОЛНОСТЬЮ <--