Контрольная работа: Економіко-математичні методи і алгоритми

,

де – кількість спостережень, ();

– кількість незалежних змінних, ();

– середня арифметична -ї незалежної змінної;

– дисперсія -ї незалежної змінної.

Результати нормалізації змінних , , подамо в таблиці:

1	0,45	10,94	5,995	-0,4207	-0,0593	-0,2458
2	1,12	8,21	6,125	0,0653	-0,4515	-0,2202
3	1,35	11,51	7,275	0,2321	0,0226	0,0059
4	1,43	10,59	6,805	0,2901	-0,1096	-0,0865
5	1,26	14,42	10,475	0,1668	0,4408	0,6351
6	1,63	14,62	9,275	0,4352	0,4695	0,3991
7	0,92	9,24	6,025	-0,0798	-0,3035	-0,2399
8	1,08	13,06	8,255	0,0363	0,2453	0,1986
9	1,43	12,97	8,375	0,2901	0,2324	0,2222
10	0,62	11,71	6,775	-0,2974	0,0514	-0,0924
11	0,38	8,95	5,735	-0,4715	-0,3452	-0,2969
12	0,69	10,01	5,825	-0,2466	-0,1929	-0,2792

Побудуємо нову -матрицю, елементами якої є нормалізовані змінні , і обчислимо кореляційну матрицю:

,

де – матриця, транспонована до матриці (елементи матриці характеризують щільність зв’язку між двома незалежними змінними; () – парні коефіцієнти кореляції). Аналізуючи значення цих коефіцієнтів, робимо припущення, що між змінними і існує сильний зв’язок.

Знайдемо визначник кореляційної матриці : ; потім визначимо критерій :

.

Для ступенів свободи і рівня значущості табличне значення критерію . Оскільки обчислене значення більше за табличне, то в моделі присутня мультиколінеарність.

Складемо розрахункову таблицю для обчислення коефіцієнтів кореляції між факторами і показником:

№	Y	X2	X3	Y2	X2 2	X3 2	YX2	YX3
1	3,08	10,54	5,495	9,4864	111,0916	30,19503	32,4632	16,9246
2	5,42	7,81	5,625	29,3764	60,9961	31,64063	42,3302	30,4875
3	7	11,11	6,775	49	123,4321	45,90063	77,77	47,425
4	7,16	10,19	6,305	51,2656	103,8361	39,75303	72,9604	45,1438
5	7,17	14,02	9,975	51,4089	196,5604	99,50063	100,5234	71,52075
6	8,5	14,22	8,775	72,25	202,2084	77,00063	120,87	74,5875
7	4,48	8,84	5,525	20,0704	78,1456	30,52563	39,6032	24,752
8	5,92	12,66	7,755	35,0464	160,2756	60,14003	74,9472	45,9096
9	7,83	12,57	7,875	61,3089	158,0049	62,01563	98,4231	61,66125
10	3,31	11,31	6,275	10,9561	127,9161	39,37563	37,4361	20,77025
11	1,67	8,55	5,235	2,7889	73,1025	27,40523	14,2785	8,74245
12	3,3	9,61	5,325	10,89	92,3521	28,35563	31,713	17,5725
Сума	64,84	131,43	80,94	403,848	1487,922	571,8083	743,3183	465,4972
Середнє	5,4033	10,9525	6,7450	33,6540	123,9935	47,6507	61,9432	38,7914

Обчислимо коефіцієнти кореляції:

;

Відповідно до обчислених коефіцієнтів кореляції, показник Y має тісніший зв’язок із змінною Х₃ порівняно із змінною Х₂ . Тому відкинемо фактор Х₂ . Будемо розглядати модель Y=Y(X₁ , X₃ ).

Для припущення про вигляд залежності побудуємо діаграми розсіювання між показником та факторами, що залишилися в моделі.

Обчислимо оцінки параметрів множинної регресії у лінійній формі:

.

Відповідно до методу найменших квадратів (МНК) оператор оцінювання параметрів моделі має вигляд

,

де 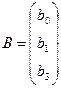; – матриця, транспонована до матриці . Матриця , крім двох векторів змінних Х₁ та Х₃ , містить вектор одиниць. Згідно з оператором оцінювання одержимо:

1) ;

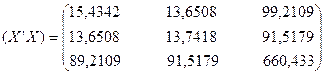2) ;

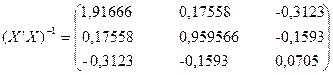3) ;

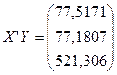4) .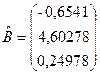