.

Оцінки параметрів моделі мають такий економічний зміст:

1) : якщо за інших рівних умов змінна Х₁ збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшується (зменшується) на 4,60278. Конкретно це означає, що збільшення (зменшення) торгової площі на 1 тис. м² приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 4,60278 млн. грн.;

2) : якщо за інших рівних умов змінна Х₃ збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшиться (зменшиться) на 0,24978. Конкретно це означає, що збільшення (зменшення) середньоденного доходу на 1 тис. грн. приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 0,24978 млн. грн.

Обчислимо суми квадратів:

.

Визначимо коефіцієнт детермінації

,

оцінений коефіцієнт детермінації

,

коефіцієнт множинної кореляції

.

Оскільки отримані значення є близькими до одиниці, то можна зробити висновок про тісний зв’язок між річним товарообігом і незалежними змінними. При цьому понад 98% варіації річного товарообігу пояснюється варіацією торгівельної площі та середньоденного доходу.

Обчислимо критерій Фішера

.

Критичне значення критерію Фішера при рівні значущості і кількості ступенів свободи та дорівнює . Порівнюючи обчислене значення критерію Фішера з критичним, робимо висновок про адекватність прийнятої математичної моделі статистичним даним.

Матриця є матрицею коваріацій оцінок параметрів моделі. Діагональні елементи цієї матриці використаємо для обчислення стандартних похибок параметрів моделі.

Знайдемо дисперсію залишків за формулою . Таким чином, . Визначимо стандартні похибки оцінок параметрів моделі, використовуючи дисперсію залишків:

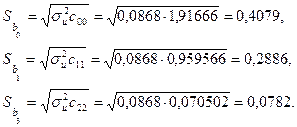
Обчислимо значення -критеріїв:

; ; .

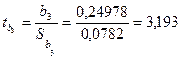Табличне значення -критерію при ступенях свободи і рівні значущості α = 0,05 становить 2,262. Всі фактичні значення -критеріїв, окрім критерію для вільного члена, перевищують за модулем табличне значення. Отже, статистично значущими є всі параметри моделі, крім вільного члена.

Визначимо коефіцієнти еластичності за формулами

, ,

де f (X ) = -0,6541 + 4,60278 X ₁ + 0,24978 X ₃ . – рівняння регресії, знайдене вище:

;

.

Отримані коефіцієнти еластичності показують, на скільки% у середньому змінюється показник Y стосовно своєї величини при зміні відповідного фактора на 1% від свого середнього значення.

Список літератури

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. шк., 1986.