Контрольная работа: Економіко-математичні методи і алгоритми
У наведеній далі задачі виконати такі дії:
1.1. записати математичні моделі прямої та двоїстої задач;
1.2. симплекс-методом визначити оптимальні плани прямої та двоїстої задач, подати їх економічний аналіз;
1.3. визначити статус ресурсів, що використовуються для виробництва продукції, та рентабельність кожного виду продукції;
1.4. обчислити інтервали стійкості двоїстих оцінок стосовно зміни запасів дефіцитних ресурсів;
1.5. розрахувати інтервали можливих змін ціни одиниці рентабельної продукції.
Підприємство виготовляє чотири види продукції, використовуючи для цього три види ресурсів. Норми витрати усіх ресурсів на одиницю продукції та запаси ресурсів наведено в таблиці. Відома ціна одиниці продукції кожного виду. Визначити план виробництва продукції, що забезпечує підприємству найбільший дохід.
| Ресурс | Норма витрат на одиницю продукції за видами | Запас ресурсу | |||
| А | В | С | Д | ||
| 1 | 2 | 1 | 1 | 1 | 280 |
| 2 | 1 | 0 | 1 | 1 | 80 |
| 3 | 1 | 5 | 0 | 0 | 250 |
| Ціна одиниці продукції (ум. од.) | 4 | 3 | 6 | 7 | |
Розв'язання:
1.1. Математичні моделі прямої та двоїстої задач мають такий вигляд:
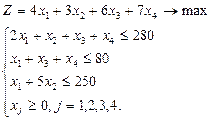
де ![]() – обсяг виробництва продукції
– обсяг виробництва продукції ![]() го виду (
го виду (![]() );
);
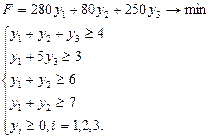
де ![]() – оцінка одиниці
– оцінка одиниці ![]() го виду ресурсу (
го виду ресурсу (![]() ).
).
Розв’яжемо пряму задачу симплекс-методом:
| Базис | Сбаз | План | 4 | 3 | 6 | 7 | 0 | 0 | 0 | |
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | ||||
| х5 | 0 | 280 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 140 |
| х6 | 0 | 80 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | |
| х7 | 0 | 250 | 1 | 5 | 0 | 0 | 0 | 0 | 1 | 250 |
| 0 | -4 | -3 | -6 | -7 | 0 | 0 | 0 | |||
| х1 | 4 | 200 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | |
| х6 | 0 | 80 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | |
| х7 | 0 | 250 | 0 | 1 | -4 | 0 | -3 | 0 | 1 | 250 |
| 560 | 0 | -3 | 10 | 2 | 4 | 0 | 0 | |||
Остання симплекс-таблиця, що відповідає оптимальному плану поставленої задачі, має вигляд:
| Базис | Сбаз | План | 4 | 3 | 6 | 7 | 0 | 0 | 0 |
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| х2 | 3 | 50 | 1 | 0 | -1 | 1 | 0 | 1 | 1/5 |
| х5 | 0 | 150 | 0 | 0 | 2 | 1 | 1 | -1 | -1/5 |
| х4 | 7 | 80 | 0 | 1 | 3/5 | 0 | 0 | 4/7 | 0 |
| 710 | 3,6 | 0 | 1 | 0 | 0 | 7 | 0,6 | ||
З наведеної симплекс-таблиці маємо:
![]()
 ;
;
min F = 80*7 +250*0,6 = 710 = max Z.
Оптимальний план прямої задачі передбачає виробництво лише двох видів продукції А і В у кількості відповідно 50 та 80 од. Випуск продукції А та С не передбачається (х1 = х3 = 0). Додаткові змінні х5 , х6 , х7 характеризують залишок (невикористану частину) ресурсів відповідно 1, 2 та 3. Оскільки х5 = 150, то перший ресурс використовується у процесі виробництва не повністю, а другий та третій ресурси – повністю (х6 = х7 =0). За такого оптимального виробництва продукції та використання ресурсів підприємство отримує найбільший дохід у розмірі 710 ум. од.
План двоїстої задачі дає оптимальну систему оцінок ресурсів, що використовуються у виробництві. Так, y2 = 7 та y3 = 0,6 відмінні від нуля, а ресурси 2 та 3 використовуються повністю. Двоїста оцінка y1 = 0 і відповідний вид ресурсу не повністю використовується при оптимальному плані виробництва. Така оптимальна система оцінок дає найменшу загальну вартість усіх ресурсів, що використовуються на підприємстві: min F = 710 ум. од.
Статус ресурсів прямої задачі можна визначити за допомогою додаткових змінних прямої задачі. Якщо додаткова змінна в оптимальному плані дорівнює нулю, то відповідний ресурс дефіцитний, а якщо відмінна від нуля – ресурс недефіцитний. В даному випадку другий та третій ресурси є дефіцитними, а перший ресурс не є дефіцитним.
Якщо запас другого дефіцитного ресурсу збільшити на 1 ум. од. ![]() , то цільова функція max Z збільшиться за інших однакових умов на y2 = 0,1 ум. од. і становитиме max Z = 710,1 ум. од. Елементи стовпчика «х6 » останньої симплекс-таблиці, який відповідає двоїстій оцінці y2 дають інформацію про зміни в оптимальному плані. У новому оптимальному плані значення змінної х4 збільшиться на 1, значення х5 збільшиться на 1,3, а значення х2 зменшиться на 2,3. Нові оптимальні значення змінних будуть такими:
, то цільова функція max Z збільшиться за інших однакових умов на y2 = 0,1 ум. од. і становитиме max Z = 710,1 ум. од. Елементи стовпчика «х6 » останньої симплекс-таблиці, який відповідає двоїстій оцінці y2 дають інформацію про зміни в оптимальному плані. У новому оптимальному плані значення змінної х4 збільшиться на 1, значення х5 збільшиться на 1,3, а значення х2 зменшиться на 2,3. Нові оптимальні значення змінних будуть такими: ![]() . Отже, збільшення запасу другого дефіцитного ресурсу за інших однакових умов приводить до зростання випуску продукції Д та зменшення випуску продукції В, а обсяг використання першого ресурсу збільшиться. За такого плану виробництва максимальний дохід підприємства буде max Z = 710,1, тобто зросте на y2 = 0,1.
. Отже, збільшення запасу другого дефіцитного ресурсу за інших однакових умов приводить до зростання випуску продукції Д та зменшення випуску продукції В, а обсяг використання першого ресурсу збільшиться. За такого плану виробництва максимальний дохід підприємства буде max Z = 710,1, тобто зросте на y2 = 0,1.
Проаналізуємо, як зміниться оптимальний план виробництва продукції, якщо запас дефіцитного ресурсу 3 за інших однакових умов збільшиться на одиницю ![]() . Аналогічно попереднім міркуванням, скориставшись елементами стовпчика «х7 » останньої симплекс-таблиці, можна записати новий оптимальний план:
. Аналогічно попереднім міркуванням, скориставшись елементами стовпчика «х7 » останньої симплекс-таблиці, можна записати новий оптимальний план: ![]() , max Z = 710 + 0,6 = 710,6 ум. од.
, max Z = 710 + 0,6 = 710,6 ум. од.
Отже, дохід підприємства збільшиться на 0,6 ум. од. за рахунок збільшення виробництва продукції В на 0,20 од.
Розрахуємо інтервали можливої зміни обсягів дефіцитних ресурсів, в межах яких двоїсті оцінки залишаються на рівні оптимальних значень.
Приріст (зміну) запасу ресурсу 2 позначимо ![]() . Тоді новий обсяг ресурсу становитиме
. Тоді новий обсяг ресурсу становитиме ![]() і новий оптимальний план
і новий оптимальний план
![]()
Єдина вимога, яку можна поставити до можливих нових оптимальних значень, – це умова невід’ємності, тобто
--> ЧИТАТЬ ПОЛНОСТЬЮ <--