Контрольная работа: Элементы статистической термодинамики
![]() - для 1 поступательной степени свободы (приближение)
- для 1 поступательной степени свободы (приближение)
 -для 3 поступательных степеней свободы 1 частицы
-для 3 поступательных степеней свободы 1 частицы
![]() - для 2 вращательных степеней свободы 1 частицы
- для 2 вращательных степеней свободы 1 частицы
(линейная молекула)
 - для 1 степени свободы вращения 1 частицы (приближение)
- для 1 степени свободы вращения 1 частицы (приближение)
 - для 3-х мерного вращения 1 частицы
- для 3-х мерного вращения 1 частицы
(общая модель)
 -для линейного осциллятора
-для линейного осциллятора
(1 колебательная степень свободы молекулы)
![]()
-Химический потенциал, отнесённый к одной частице (Внимание! не к молю!)
Химический потенциал и мольная концентрация.
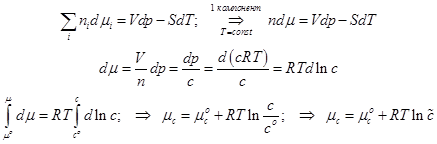
Химическое сродство и константа равновесия
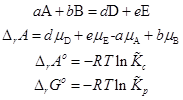
Константа химического равновесия в смеси идеальных газов
Рабочие формулы:
Вариант 1. Здесь представлены электронные суммы состояний. Их следует вычислять по отдельности. Электронные уровни должны быть выражены в единой шкале. Этот способ строгий, но менее доступный:
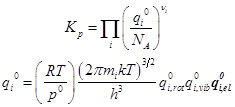
Вариант 2. Здесь представлены кратности вырождения электронных уровней и разность электронных уровней. Этот способ удобен для расчёта диссоциативных равновесий:

(ВНИМАНИЕ! В учебнике Даниэльса и Олберти в формулах допущены ошибки, связанные с учётом электронных состояний. Здесь ошибки исправлены)
ЗАДАЧИ (с примерами решений) (из Даниэльса – Олберти и из задачника МГУ - Ерёмин и соавторы – см. Литература)
ЗАДАЧА 1.
У молекулы с массой M четыре квантовых состояния распределены между двумя энергетическими уровнями. Спектр уровней определён в виде массива: (0, E, E, E).
Нарисуйте энергетическую диаграмму состояний.
Как называют подобные уровни?
Каковы средние мольные доли частиц, заселяющих эти уровни при температуре T?
Сколько частиц в среднем будет заселять эти уровни в коллективе из N частиц?
Какова поступательная энтропия газа с этими характеристиками в объёме V?