Контрольная работа: ЭММ и М

Тогда соотношения (4) для нашего примера перепишутся следующим образом:

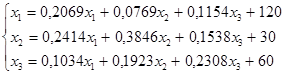
Данная система одновременных уравнений представляет собой модель для решения задачи 1.3.

1.4. Поскольку увеличение цены на продукцию второй отрасли в 2 раза является инфлятогенным фактором в экономике, произойдет повышение цен на продукцию первой и третьей отраслей. Обозначим индекс роста цен на продукцию первой отрасли р₁ , третьей отрасли – р₃ . Построение модели осуществляется с целью нахождения индексов р₁ и р₃ при условии, что р₂ = 2 и соответствующих ограничений на рост заработной платы. Очевидно, что инфляционные процессы вызовут изменение номинальных потоков МОБ. Исходя из экономического смысла показателей отчетного МОБ, в новых ценах I и III квадранты МОБ перепишутся как представлено в таблице 3.

Таблица 2.

Показатели I и III квадрантов МОБ

в новых ценах (млн.руб.)

отрасли-производители	отрасли-потребители
	1	2	3
1	30*р1	10*р1	15*р1
2	35*2	50*2	20*2
3	15*р3	25*р3	30*р3
зарплата	19,5*р1 *0,7	13,5*2*0,7	19,5*р3 *0,7
прочие элементы добавленной стоимости	45,5*р1	31,5*2	45,5*р3
валовый выпуск	145*р1	130*2	130*р3

Поскольку индекс цен на продукцию второй отрасли равен 2 и величина затрат на продукцию второй отрасли не влияет на формирование цены в этой отрасли, то баланс описывается для первой и третьей отрасли. Модель строится с использованием балансовых соотношений (2) в новых ценах:

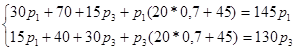
Данная система одновременных уравнений представляет собой балансовую модель для решения задачи (1.4). Поскольку в дальнейшем система будет решатся на ПЭВМ и использованием стандартного ППП, необходимо провести подобные и записать модель в стандартном виде:

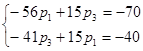
1.5. Задача решается аналогично решению задачи 1.4. Отличительной особенностью данной задачи является то, что инфлятогенным фактором выступает рост заработной платы на 50% в третьей отрасли, хотя в остальных отраслях зарплата остается неизменной. Данный фактор вызовет рост цен на продукцию отраслей соответственно в р₁ , р₂ , р₃ раз. В новых ценах показатели I и III квадрантов МОБ представлены в табл. 4.

Таблица 3.

Показатели I и III квадрантов МОБ

в новых ценах (млн.руб.)

отрасли-производители	отрасли-потребители
	1	2	3
1	30*р1	10*р1	15*р1
2	35*р2	50*р2	20*р2
3	15*р3	25*р3	30*р3
зарплата	19,5*1	13,5*1	19,5*1,5
прочие элементы добавленной стоимости	45,5*р1	31,5*р2	45,5*р3
валовый выпуск	145*р1	130*р2	130*р3

С учетом указанных условий соотношения МОБ (2) запишутся:

Система уравнений представляет собой балансовую модель для решения задачи (1.5). После при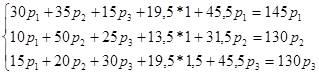
ведения подобных модель имеет вид:

3. Задача №2.

2.1. Для определения вида зависимости построим диаграмму рассеяния по имеющимся данным.

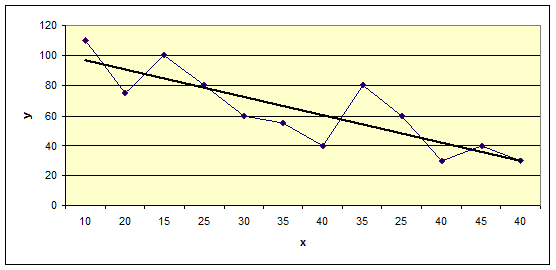
Рис.1. Диаграмма рассеяния и регрессионная прямая, отражающая зависимость инвестиций от объема производства

Расположение точек на диаграмме рассеяния позволяет предположить линейную связь между прибылью предприятия и ставкой налога. Поэтому имеет смысл искать зависимость в виде линейной функции: ŷ = b₀ + b₁ х. Очевидно также, что данная зависимость прямая: с увеличением ставки налога прибыль уменьшается.

2.2. В нашем примере при использовании МНК минимизируется следующая функция , т.е. сумма квадратов отклонений эмпирических значений у_i от расчетных значений ŷ_i должно быть минимальным. Согласно МНК для нашего примера воспользуемся следующими формулами расчета:

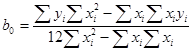
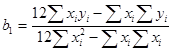
Для нахождения оценок параметров b₀ и b₁ в ручном режиме составим рабочую таблицу, которая содержит исходные данные и промежуточные результаты.

Таблица 4.

Рабочая таблица вычисления оценок параметров уравнения регрессии при изучении зависимости инвестиций от объема производства

I	x	y	x*2	x*y	y2	Yср	e	e2	e/y*100	(x-x ср)2	(у-уср)2	(е-е1)	(е-е)2
1	10	110	100	1100	12100	105,92	4,08	16,65	3,71	400	2177,78	-	-
2	20	75	400	1500	5625	84,62	-9,62	92,54	12,83	100	136,11	-13,7	187,69
3	15	100	225	1500	10000	95,27	4,73	22,37	4,73	225	1344,69	14,35	205,92
4	25	80	625	2000	6400	73,97	6,03	36,36	7,54	25	277,89	1,3	1,69
5	30	60	900	1800	3600	63,32	-3,32	11,02	5,53	0	11,089	-9,35	87,42
6	35	55	1225	1925	3025	52,67	2,33	5,43	4,24	25	69,39	5,65	31,92
7	40	40	1600	1600	1600	42,02	-2,02	4,08	5,05	100	544,29	-4,35	18,92
8	35	80	1225	2800	6400	52,67	27,33	746,93	34,16	25	277,89	29,35	861,42
9	25	60	625	1500	3600	73,97	-13,97	195,16	23,28	25	11,09	-41,3	1705,69
10	40	30	1600	1200	900	42,02	-12,02	144,48	40,07	100	1110,89	1,95	3,80
11	45	40	2025	1800	1600	31,37	8,63	74,48	21,58	225	544,29	20,65	426,42
12	40	30	1600	1200	900	42,02	-12,02	144,48	40,07	100	1110,89	-20,65	426,42
Сумма	360	760	12150	19925	55750	759,84		1493,98	202,78	1350	7616,29	-16,1	259,21
среднее	30,00	63,33	1012,50	1660,42	4645,83	63,32	0,00	124,50	16,90	112,50	634,69	-1,34	21,60

Согласно формулам имеем: