Контрольная работа: ЭММ и М
Таким образом, регрессионная модель имеет вид: ŷ=127,22+(-2,13)х.
у1 = 127,22+(-2,13)*10= 105,92
Для анализа силы линейной зависимости прибыли от ставки налога найдем коэффициент корреляции по формуле:
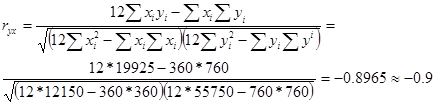
Данное значение коэффициента корреляции позволяет сделать вывод о том, что связи между прибылью и ставкой налога не чуществует.
Средняя относительная ошибка аппроксимации для нашего примера рассчитывается как среднеарифметическая относительных отклонений по каждому наблюдению:
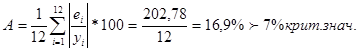
2.3. Стандартная ошибка регрессии характеризует уровень необъясненной дисперсии и для однофакторной линейной регрессии (m=1) рассчитывается по формуле:
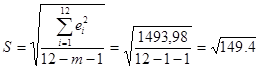
Стандартная ошибка параметра b1 уравнения регрессии находится по формуле:
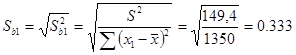
Стандартная ошибка параметра b0 определяется:
![]()
На основе стандартных ошибок параметров регрессии проверим значимость каждого коэффициента регрессии путем расчета t-статистик и их сравнении с критическим значением при уровне значимости α=0,05 и числом степеней свободы (12-m-1)=10: tкр =![]()
![]()
![]()
Поскольку tb 1 = -6,396<2,228, не подтверждается статистическая значимость коэффициента регрессии b1 .
Поскольку tb 0 =12,75 >2,228, гипотеза о статистической незначимости коэффициента b0 отклоняется. Это значит, что в данном случае нельзя пренебречь свободным членом уравнения регрессии, рассматривая уравнение:
у=127,22-2,13*х
Коэффициент детерминации в нашем случае рассчитывается по формуле:
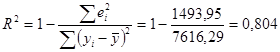
Поскольку R2 =0,804<12,75, то можно заключить, что введенный в регрессию фактор – ставка налога- не объясняет поведение показателя – прибыль.
Для оценки автокорреляции остатков рассчитываем значение критерия Дарбина-Уотсона по формуле:
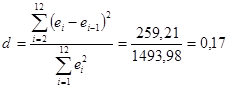
Поскольку значение d меньше 2, то это позволяет сделать предположение о положительной автокорреляции остатков.
Запись полученных характеристик уравнения в стандартной форме имеет вид:
У=127,22-2,13х; rху =-0,9; R2 =0,804; DW=0,17; А=16,9%
Стандарт ошибка (0,333) (9,98)
t-стат. (-6,396) (12,75)