Контрольная работа: Идентификация объекта управления
![]() .
.
Пример
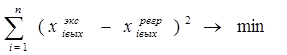
Рассмотрим пример использования метода наименьших квадратов. Пусть выходной сигнал (функция отклика) зависит от одного фактора (входного сигнала). Активно проведено n экспериментов. Задана ![]() и получена
и получена ![]() – результатов экспериментов. Общий вид уравнения регрессии 1-го порядка для примера:
– результатов экспериментов. Общий вид уравнения регрессии 1-го порядка для примера:
xвых = b0 + b1 x1
Методом наименьших квадратов ищем минимум функции Ф:
![]()
Для получения минимума этой Ф приравниваем к нулю частные производные
![]() .
.
Для удобства получения частных производных введем фиктивную переменную x0 =1 и функцию Ф запишем:
![]()

x0 =1 можно убрать. Тогда

Решая эту систему алгебраических уравнений (можно методом Крамера), находим:


Проверка идентичности математической модели – уравнения регрессии исследуемого объекта проводится по нескольким критериям адекватности и идентичности модели.
Поскольку результаты опытов в эксперименте заранее точно предсказать невозможно, то обработка и сами результаты связаны с неопределенностью или вероятностью. Вероятность изменяется в пределах: 0 – события быть не может, 1 – событие произойдет обязательно (день-ночь). При большом числе параллельных (одинаковые условия) опытов вероятность может быть задана в виде функции распределения вероятностей (рис. 4.):

Рис. 4. Схема нормального (гауссовского) закона распределения вероятностей
На практике чаще всего используется так называемое нормальное (гауссовское) распределение вероятностей.
Случайная величина (![]() ) имеет несколько числовых характеристик, наиболее важные из которых – это математическое ожидание и дисперсия.
) имеет несколько числовых характеристик, наиболее важные из которых – это математическое ожидание и дисперсия.
Математическое ожидание – это среднее взвешенное значение случайной величины
![]()
Дисперсия характеризует разброс значений случайной величины относительно ее математического ожидания.
![]() .
.
Проверка значимости уравнения регрессии проводится по критерию Фишера или F-критерию. Проверка заключается в определении, значимо ли (больше ошибки измерения) полученное уравнение ![]() отличается от уравнения
отличается от уравнения ![]() . Для этого вычисляют дисперсию относительно среднего значения выходного сигнала:
. Для этого вычисляют дисперсию относительно среднего значения выходного сигнала:
 ,
,
где f1 – число степеней свободы,