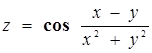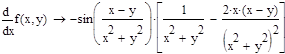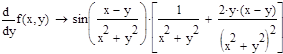Контрольная работа: Изучение матриц
или
соответственно.
19. Что такое частное приращение функции нескольких переменных?
Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных 
в точке 
частные производные определяются так:
,
,
если эти пределы существуют.
Из определения следует геометрический смысл частной производной функции двух переменных: частная производная 
– угловой коэффициент касательной к линии пересечения поверхности и плоскости 
в соответствующей точке .
20. Каковы выражения для частных дифференциалов функции z = f ( x , y )?
Частной производной по x функции z = f (x , y ) в точке M 0 (x 0 , y 0 ) называется предел 
,
если этот предел существует . Обозначается эта частная производная любым из следующих символов:
;
;
.
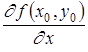Частная производная по x есть обычная производная от функции z = f (x , y ), рассматриваемой как функция только от переменной x при фиксированном значении переменной y .
Совершенно аналогично можно определить частную производную по y функции z = f (x , y ) в точке M 0 (x 0 , y 0 ):
=
.
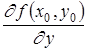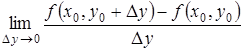Приведем примеры вычисления частных производных
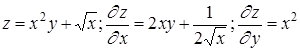
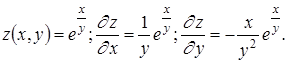
21. Каково выражение для полного дифференциала функции u = u ( x , y , z )?
Полный дифференциал du функции u = f (x, y, z) (если он существует) равен сумме всех ее частных дифференциалов:
22. Напишите частные производные третьего порядка для функции z = f ( x , y , z )
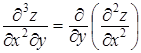
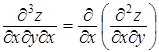
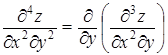
23. Найти частную производную и частный дифференциал функции. 
