Для оценки начальных значений а (0) и b (0) применим линейную модель к первым 8 значениям Y ( t ) из табл. 1. Линейная модель имеет вид:

. (5)

Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения а (0) и b (0) по формулам 6 - 9:

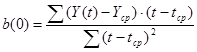; (6)

; (7)

; (8)

. (9)

Применяя линейную модель к первым 8 значениям ряда из таблицы 1 (т.е. к данным за первые 2 года), находим значения а (0) и b (0). Составим вспомогательную таблицу для определения параметров линейной модели:

Таблица 2

t		Y(t)	t-tcp	Y-Ycp	(t-tcp )2	(Y-Ycp )(t-tcp )
1		28	-3,5	-7,625	12,25	26,6875
2		36	-2,5	0,375	6,25	-0,9375
3		43	-1,5	7,375	2,25	-11,0625
4		28	-0,5	-7,625	0,25	3,8125
5		31	0,5	-4,625	0,25	-2,3125
6		40	1,5	4,375	2,25	6,5625
7		49	2,5	13,375	6,25	33,4375
8		30	3,5	-5,625	12,25	-19,6875
S	36	285	0	0	42	36,5

Уравнение (5) с учетом полученных коэффициентов имеет вид: Y_p ( t ) =31,714+0,869·t . Из этого уравнения находим расчетные значения Y _р ( t ) и сопоставляем их с фактическими значениями (табл. 3). Такое сопоставление позволяет оценить приближенные значения коэффициентов сезонности I-IV кварталов F (-3) , F (-2) , F (-1) и F (0) для года, предшествующего первому году, по которому имеются данные в табл. 1. Эти значения необходимы для расчета коэффициентов сезонности первого года F (1), F (2), F (3), F (4) и других параметров модели Хольта-Уинтерса по формулам 1 - 4.

Таблица 3

Сопоставление фактических данных Y ( t ) и рассчитанных по линейной модели значений Y_p ( t )

t	1	2	3	4	5	6	7	8
Y(t)	28	36	43	28	31	40	« 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 344 Бесплатно скачать Контрольная работа: Кредиты от коммерческого банка на жилищное строительство >>> Скачать <<< Меню Поиск