Контрольная работа: Криволинейный интеграл первого и второго рода
в) указанием направления интегрирования (рис. 2).
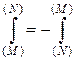
![]()
![]()
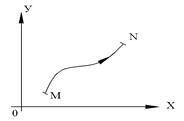
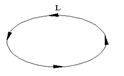
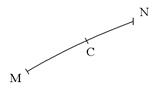
Рис. 2
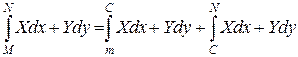
![]() -можно рассматривать как интеграл от векторной функции
-можно рассматривать как интеграл от векторной функции ![]()
Тогда 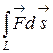 - если
- если ![]() -замкнутая то
-замкнутая то 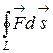 -называют циркуляцией вектора
-называют циркуляцией вектора ![]() по контуру
по контуру ![]() .
.
30 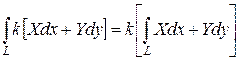
40 ![]() не зависит от того какую точку
не зависит от того какую точку ![]() взять за начало
взять за начало![]()
Вычисление криволинейного интеграла
Криволинейные интегралы вычисляются сведением их к обыкновенным интегралам по отрезку прямой (рис. 3).
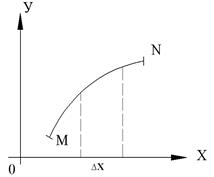
Рис. 3
![]() -гладкая кривая.
-гладкая кривая.

1. Если ![]() -непрерывны,
-непрерывны, ![]() -непрерывные.
-непрерывные.
![]() -непрерывны по
-непрерывны по ![]() , то
, то 
Пределы А и В не зависят ни от способа деления ![]() на
на ![]() , ни от вектора
, ни от вектора ![]()
![]()

![]()

Следовательно:  .
.


2. В случае: 



1. Формула Грина.