Контрольная работа: Криволинейный интеграл первого и второго рода

Теорема: -непрерывны в области , тогда для того, чтобы

в (рис. 6)

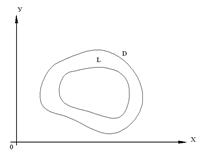
Рис. 6

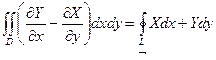
Пусть

Обратно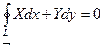

Т.д.

Пусть из непрерывности и

-окрестность точки такая что в

предположение неверно. ч.т.д.

Замечание.

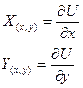
Определение. Функция -градиент которой есть вектор силы называется потенциалом вектора .

Тогда

Вывод: Криволинейный интеграл от полного дифференциала не зависит от формы пути интегрирования.

Литература

1. Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ. 1-2 том. Изд. МГУ, 1989 г.

2. Виноградова И.А., Олексич С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. Часть 1,2 Изд. МГУ. Серия классический университетский учебник 250 летию МГУ 2005 г.

3. Шилов Г.Е. Математический анализ. Часть 1,2. Москва. Изд. Лань. 2002 г. – 880 с.

4. Лунгу К.Н. Сборник задач по математике. Часть 1,2. Москва. Айрис пресс 2005 г.