Контрольная работа: Криволинейный интеграл первого и второго рода

Криволинейный интеграл первого рода

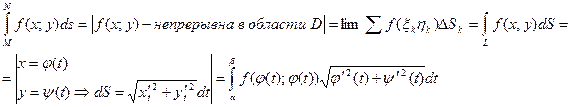
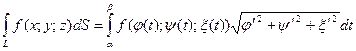
Криволинейный интеграл второго рода

1. Задача приводящая к понятию криволинейного интеграла.

Определение криволинейного интеграла по координатам.

2. Свойства криволинейного интеграла (рис. 1).

3. Вычисления

а)

б)

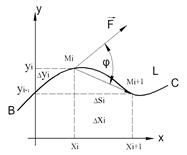
Рис. 1

Займемся обобщением понятия определенного интеграла на случай когда путь интегрирования – кривая -кривая , , . Т/н. А-работу силы при перемещении точки от к

1. Разобьем на n частей :

Обозначим вектор- хорда дуге.

Пусть предположим, что на тогда

Работа вдоль дуги вычисляется как скалярное произведение векторов и

Пусть

Тогда:

Работа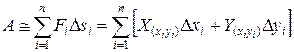

Если 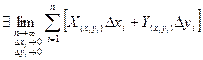, то этот предел примем за работу А силы при движении точки по кривой от точки до точки

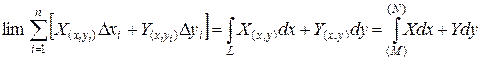
,-не числа, а точки концы линии .

1. Свойства:

1⁰ определяется

а) подынтегральным выражением

--> ЧИТАТЬ ПОЛНОСТЬЮ <--