Контрольная работа: Линейная алгебра и математическое программирование
40
15
6
160
4
200
250
25
20
10
10
240
15
18
Число занятых клеток в таблице, приведенной выше, равно m + n – 1 = 5 + 3 – 1 = 7, то есть условие невырожденности выполнено. Получили исходное решение, которое запишем в виде матрицы
Х1 =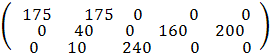
Стоимость перевозки при исходном решении составляет
f1 = 175 * 5 + 175 * 15 + 40 * 10 + 160 * 6 + 200 * 4 + 10 * 20 + 240 * 10 = 8260.
Проверим найденное решение транспортной задачи на оптимальность Найденное исходное решение проверяется на оптимальность методом потенциалов по следующему критерию: если решение транспортной задачи является оптимальным, то ему соответствует система m+n ( 5 + 3 = 8 ) действительных чисел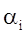 
и 
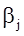, удовлетворяющих условиям 
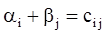для занятых клеток и 
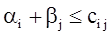– для свободных клеток.
Числа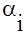 
и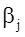 
называются потенциалами. В распределительную таблицу добавляют столбец 
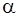и строку 
.
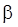Потенциалы 
и 
находят из равенства 
, справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например 
, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал 
, то 
; если известен потенциал , то 
.
Обозначим 
. Эту оценку называют оценкой свободных клеток. Если 
, то опорное решение является оптимальным. Если хотя бы одна из оценок 
, то решение не является оптимальным и его можно улучшить, перейдя от одного решения к другому.
Проверим найденное решение на оптимальность, добавив в распределительную таблицу, приведенную ниже, столбец 
и строку 
.
Полагая 
, запишем это значение в последнем столбце
таблицы.
|
ai | 1 | 2 | 3 | 4 | 5 | |
| 175 | 225 | 240 | 160 | 200 | 𝛼i | |
|
1 | 350 |
5 175 |
15 175 |
К-во Просмотров: 326
Бесплатно скачать Контрольная работа: Линейная алгебра и математическое программирование
| ||
bi