Контрольная работа: Линейное программирование
2×450 + 5×100 = 1400 < 1600
Условия дополняющей нежесткости (вторая теорема двойственности): для оптимальных планов двойственных задач имеют место соотношения:
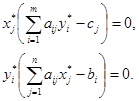
Так как для оптимального решения прямой задачи треть ограничение выполняется как неравенство, то в оптимальном решении двойственной задачи y3 = 0.
Так как для оптимального решения прямой задачи х1 > 0и х2 > 0, то оба ограничения двойственной задачи выполняются как равенство. Для нахождения решения двойственной задачи получаем систему
![]() y3 = 0
y3 = 0
y1 + 2y2 + 2y3 = 3
y1 + 3y2 + 5y3 = 4
Получаем решение: y1 =, y2 = 1, y3 = 0.
Найдем значение целевой функции двойственной задачи:
g(Y) = 550×1 + 1200×1 + 1600×0 = 1750.
Получили gmin = fmax = 1750 ден. единиц.
Так как значения прямой и двойственной функций равны, то Y = (1; 1; 0) является оптимальным решением двойственной задачи (по первой теореме двойственности).
Задача 3.
Задание 1. Записать исходные данные задачи в виде транспортной таблицы, определить, открытой или закрытой является транспортная задача.
Задание 2. Сформулировать экономико-математическую модель исходной транспортной задачи.
Задание 3. Найти оптимальный план перевозок, отметив при этом единственность или неединственность оптимального плана.
Вариант 3.
На складах A, B, C, Д находится соответственно 50 т, 40 т, 40 т и 70 т муки, которую нужно доставить четырем хлебозаводам. Первому хлебозаводу требуется 50 т муки, второму – 40 т, третьему – 50 т и четвертому – 60 т муки. Стоимость доставки одной тонны муки со склада А каждому хлебозаводу соответственно равны 8, 3, 5 и 2 ден. единиц, со склада В – 7, 4, 9 и 8 ден. единиц, со склада С – 6, 3, 3 и 1 ден. единиц, со склада Д – 2, 4, 1 и 5 ден. единиц. Составить план перевозки муки, обеспечивающий минимальные транспортные расходы.
Решение.
Задание 1.
|
Мощности поставщиков |
Мощности потребителей | |||
|
50 |
40 |
50 |
60 | |
|
50 |
К-во Просмотров: 1126
Бесплатно скачать Контрольная работа: Линейное программирование
| |||