Контрольная работа: Линейное программирование

2x₁ + 3x₂ £ 1200

2x₁ + 5x₂ £ 1600

x₁ , x₂ ³ 0, целые.

Задание 2.

Решаем задачу без условия целочисленности решения. Построим множество допустимых решений задачи.

Прямые ограничения x_1,2 ³ 0 выделяют первую четверть плоскости.

Проведем прямую x₁ + x₂ = 550 через точки (0; 550) и (550; 0). Подставим в первое неравенство координаты точки (0; 0): 1×0 +1×0 = 0 < 550, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.

Проведем прямую 2x₁ + 3x₂ = 1200 через точки (0; 400) и (600; 0). Подставим в первое неравенство координаты точки (0; 0): 2×0 + 3×0 = 0 < 1200, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.

Проведем прямую 2x₁ + 5x₂ = 1600 через точки (0; 320) и (800; 0). Подставим в первое неравенство координаты точки (0; 0): 2×0 + 5×0 = 0 < 1600, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.

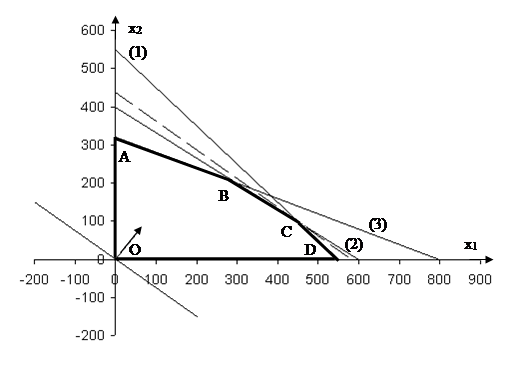
Множество допустимых решений – это многоугольник ABCDO.

Построим линию уровня целевой функции f(X) = 3x₁ + 4x₂

3x₁ + 4x₂ = 0 через точки (200; -150 ) и (-200; 150).

Вектор-градиент {3; 4} задает направление, перемещаясь вдоль которого, можно увеличить значение целевой функции; перемещаясь в противоположном направлении, можно уменьшить ее значение. На чертеже построен вектор, пропорциональный градиенту (60; 80), так как сам градиент имеет малый масштаб на чертеже.

Из чертежа видно, что наибольшее значение целевой функции будет на линии уровня, проходящей через точку С, являющейся пересечением прямых (1) и (2).

Координаты этой точки найдем из системы

x₁ + x₂ = 550,

2x₁ + 3x₂ = 1200.

Первое уравнение умножим на 2 и вычтем из второго, получаем x₂ = 100 и x₁ = 450

f_mах = 3 ×450 + 4 ×100 = 1750 ден. единиц.

Полученное оптимальное решение оказалось целым, следовательно, это решение поставленной задачи. Получили: в оптимальном плане выпуска следует произвести полок типа А 450 шт., а полок типа Б – 100 шт.При этом прибыль от реализации составит 1750 ден. единиц и будет наибольшей.

Задание 3.

Двойственная задача.

Найти минимум функции g(Y) при ограничениях:

g(Y) = 550y₁ + 1200y₂ + 1600y₃ ® min

y₁ + 2y₂ + 2y₃ ³ 3

y₁ + 3y₂ + 5y₃ ³ 4

y_1,2,3 ³ 0.

Оптимальное решение прямой задачи Х = (450; 100). Подставим его в ограничения этой задачи

1×450 + 1×100 = 550