Контрольная работа: Логарифмічно-лінійний аналіз
1. Основні поняття логлінійного аналізу
2. Аналіз зв’язку категоризованих змінних
3. Канонічна кореляція при аналізі таблиць спряженості ознак
4. Побудова логарифмічної моделі
Висновки
Список використаних джерел
1. Основні поняття логлінійного аналіза
Останніми роками активно розробляються методи аналізу таблиць спряженості ознак. Це пояснюється в першу чергу наявністю некількісних (так званих якісних) величин в описі соціально-економічних об'єктів, потребами вивчення зв'язків між ними. Таблиця спряженості є універсальною формою подання даних, яка не пов'язана з рівнем вимірювання ознак. Будь-яку величину можна представити як категоризовану.
В медичних дослідженнях частіше реєструються величини, які оцінюються якісно. Тоді при спостереженні n об'єктів, кожні з k ознак, що описують ці об'єкти, подаються у вихідній матриці кодами їх категорій (рівнів). За даною вихідною матрицею спостережень одержують таблицю спряженості, яка включає частоти спостережень при всіх комбінаціях рівнів ознак.
Одним з основних питань, яке виникає при обробці даних, є питання про наявність взаємозв'язку між ознаками. Методом багатовимірного статистичного аналізу, який використовується для обробки багатовимірних таблиць спряженості, є логлінійний аналіз.
Основна ідея логлінійного аналізу полягає в тому, що в кожній комірці таблиці спряженості записується розклад натурального логарифма частоти на суму ефектів всіх взаємозв'язків досліджуваних ознак. Модель к-го порядку називається насиченою , якщо вона крім головних ефектів містить будь-які взаємозв'язки величин від другого до к-го порядків включно. Так, наприклад, для 3-х факторів A, B, C насичена модель має вигляд:
![]() (1.1)
(1.1)
де μ - загальне середнє,![]() - головні ефекти досліджуваних ознак. Так, наприклад,
- головні ефекти досліджуваних ознак. Так, наприклад, ![]() можна інтерпретувати як додаток (спад, якщо її знак від’ємний) i-ой категорії фактора A в порівнянні із загальним середнім, що є мірою того, наскільки ймовірна i-а категорія ознаки А в порівнянні з іншими;
можна інтерпретувати як додаток (спад, якщо її знак від’ємний) i-ой категорії фактора A в порівнянні із загальним середнім, що є мірою того, наскільки ймовірна i-а категорія ознаки А в порівнянні з іншими; ![]() - ефекти відповідних взаємодій. Насичена модель містить стільки ж параметрів, скільки і комірок в таблиці спряженості. Для того, щоб модель була не надлишковою, тобто, щоб число параметрів не перевищило число елементів (
- ефекти відповідних взаємодій. Насичена модель містить стільки ж параметрів, скільки і комірок в таблиці спряженості. Для того, щоб модель була не надлишковою, тобто, щоб число параметрів не перевищило число елементів (![]() ) досліджуваної таблиці спряженості, на значення в моделі накладаються наступні обмеження:
) досліджуваної таблиці спряженості, на значення в моделі накладаються наступні обмеження:
![]()
(1.2)
Сенс дослідження полягає в тому, щоб знайти найбільш економне пояснення даних, представлених в таблиці спряженості (найбільш просту структуру). Окрім насичених моделей часто використовують ієрархічні моделі, які отримують з насичених шляхом послідовного виключення ефектів, що не є значущими. При ієрархічній побудові включення в модель взаємодій к-го порядку вимагає включення всіх взаємодій нижчого порядку, а також всіх головних ефектів. Як і в регресійному аналізі для виключення неістотних дій можуть застосовуватися методи покрокового включення і покрокового виключення змінних. В результаті видалення неістотних ефектів можуть мати місце наступні види моделей:
1) ![]() - такі моделі називаються моделями незалежності . Вони містять лише головні ефекти, відсутні ефекти взаємодії чинників.
- такі моделі називаються моделями незалежності . Вони містять лише головні ефекти, відсутні ефекти взаємодії чинників.
2) ![]() - категорії факторів В і С – рівноймовірні.
- категорії факторів В і С – рівноймовірні.
3) ![]() - категорії факторів А і С – рівноймовірні.
- категорії факторів А і С – рівноймовірні.
4) ![]() - категорії факторів В і А – рівноймовірні.
- категорії факторів В і А – рівноймовірні.
5) ![]() - всі категорії всіх факторів – рівноймовірні.
- всі категорії всіх факторів – рівноймовірні.
6) ![]() - має місце взаємозв'язок двох ознак А і В. Така модель не відноситься до ієрархічних.
- має місце взаємозв'язок двох ознак А і В. Така модель не відноситься до ієрархічних.
7) ![]() - має місце взаємозв'язок двох ознак В і С.
- має місце взаємозв'язок двох ознак В і С.
2. Аналіз зв’язку категоризованих змінних
Дуже часто вивчення взаємозв'язків між якісними змінними зводитися до аналізу двох змінних х і у, які набувають низку значень – х1 , …, хm і y1 ,…, yp . Позначимо номер рядка двовимірної таблиці через і (і = 1,…,m), номер стовпця – через j (j = 1,…,р). Кожен об'єкт характеризується значеннями двох змінних хi і yj . У комірках таблиці записується число об'єктів у вибірці, що володіють даним поєднанням значень ознак (коміркова частота) – nij .
Як правило, аналіз двовимірних таблиць спряженості обмежується висновками про наявність зв'язку і її тісноти. Класичним тестом, який використовується для встановлення факту наявності зв'язку, є критерій χ2 . Величина χ2 звичайно визначається як сума квадратів між фактичними (nij ) і теоретичними (![]() ) частотами двовимірного розподілу, поділена на теоретичні частоти.
) частотами двовимірного розподілу, поділена на теоретичні частоти.
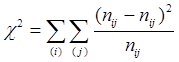 (2.1)
(2.1)
Нульовою гіпотезою є: ![]() . Розрахунок очікуваних частот двовимірного розподілу проводиться в припущенні про статистичну незалежність змінних
. Розрахунок очікуваних частот двовимірного розподілу проводиться в припущенні про статистичну незалежність змінних
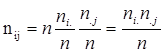 (2.2)
(2.2)
де ![]() - сума за і-тим рядком таблиці,
- сума за і-тим рядком таблиці, ![]() - сума за j-м стовпцем таблиці (так звані маргінальні частоти ). Обираючи рівень значущості λ, визначають відповідне критичне значення критерію χ2 λ;df при числі ступенів вільності df = (m - 1)(p - 1). Якщо розрахункова величина χ2 перевищує критичне значення χ2 λ;df , то на даному рівні значущості нульова гіпотеза Н0 може бути відхилена.
- сума за j-м стовпцем таблиці (так звані маргінальні частоти ). Обираючи рівень значущості λ, визначають відповідне критичне значення критерію χ2 λ;df при числі ступенів вільності df = (m - 1)(p - 1). Якщо розрахункова величина χ2 перевищує критичне значення χ2 λ;df , то на даному рівні значущості нульова гіпотеза Н0 може бути відхилена.
Аналіз якісних змінних передбачає використання багатовимірних методів. Існуючі взаємозв'язки між змінними вимагають їх спільного розгляду, переходу від парних зв'язків до аналізу множинних і частинних зв'язків, від двовимірних таблиць спряженості до складних комбінаційних таблиць. Ця потреба добре усвідомлюється дослідниками, але проте часто не реалізується.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--