Контрольная работа: Логарифмічно-лінійний аналіз

Відповідно є можливість подати вихідну таблицю спряженості у вигляді серії таблиць, кожна з яких відповідає певній гіпотезі зв'язку змінних (тобто частоти таблиці, обчислені при тому або іншому власному числі λ_k матриці С).

Існує ряд способів знаходження канонічних міток. Найшвидше приводить до мети наступний порядок дій: спочатку визначаються х_ik діленням кожної компоненти відповідного власного вектора на корінь квадратний з маргінальної частки; потім визначаються y_jk – шляхом усереднювання міток рядків для кожного j - й стовпця.

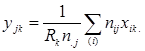(3.10)

Набори міток х_ik і y_jk , зважені за відповідними маргінальними частотами, мають нульові середні й одиничні дисперсії.

4. Побудова логарифмічної моделі

Логарифмічно лінійна модель системи з трьох змінних запишеться у вигляді:

λ_ijk ^ABC (4.1)

де ln(n_ijk ) – очікувана частота чарунка (і, j, k) тривимірної таблиці спряженості, обчислена за умови незалежності змінних A, B, C; параметри λ визначають внесок у логарифм очікуваної частоти змінних як окремо , так і внаслідок їхньої взаємодії. Параметри λ логлінійної моделі задовольняють умовам:

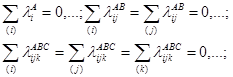(4.2)

Оцінки параметрів обчислюються за методом максимальної правдоподібності:

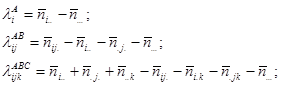(4.3)

Точка в індексі означає середнє значення за цим індексом, так:

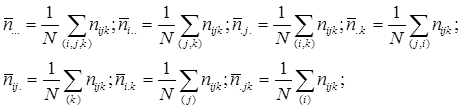(4.4)

де n_ijk - частота комірки (і, j, k), яка спостерігається N – число комірок таблиці спряженості.

Оцінка дисперсії параметра λ для насиченої моделі дорівнює

(4.5)

де δ_ii ^ZA = 1, якщо А належить групі змінних Z и , в супротивному разі δ_ii ^ZA = 0. Аналогічно обчислюються δ_jj ^ZB , δ_kk ^ZC .

Якщо поділити, знайдену в результаті розрахунків оцінку на оцінку його середнє квадратичного відхилення , то одержимо стандартизоване значення оцінки параметра. Це значення може бути використане для порівняння відносного внеску кожного параметра в n_ijk , тим самим для обчислення порівняльного значення впливу окремих змінних, кожному парний і множинному взаємозв'язки.

Відзначається, що, крім з насиченої моделі стандартизовані параметри , рівні нулю, можна перейти до моделі, більш адекватної вихідних даних або апріорним припущенням про відносини між змінними.

Одержуємо модель ієрархічну за побудовою, оскільки модель врахована множинна взаємодія A, B, C, а це означає припущення існування зв'язків у будь-якій підгрупі зі складових "старших" взаємозв'язок (ABC) змінних, і тому в модель включені такі параметри, як λ^AB , λ^BC , λ^AC , λ^A , λ^B , λ^C . Якщо ж передбачається, що між змінними немає взаємозв'язків, то у модель не включається відповідний параметр λ . Порядок логлинейной моделі дорівнює найбільшому числу змінних.

Побудова моделі складається з наступних основних етапів: 1) означення порядку логлінійної моделі; 2) відбір параметрів заданого порядку для включення в підсумкову модель.

Логлінійна модель має порядок к, якщо будь-які до к + 1 і більше змінних одночасно незалежні. Тому для означення порядку моделі перевіряються гіпотези про незалежність будь-яких до к + 1 і більш змінних за допомогою критеріїв и (максимальної правдоподібності). Число ступенів вільності для обох статистик дорівнює n-p, де n – число всіх комірок таблиці, а p – число оцінюваних очікуваних частот за умови незалежності змінних.

Крім того, для кожного к-го порядку перевіряється гіпотеза про одночасну незалежність відповідних ним змінних за допомогою цих же критеріїв.

Так, для параметрів третього порядку перевіряється гіпотеза про відсутність потрійної взаємодії.

Спільна перевірка викладених вище гіпотез дозволяє визначити порядок моделі, що щонайкраще відбиває структуру взаємозв'язків змінних.

Наступним етапом є відбір параметрів моделі, тобто включення в модель тільки тих параметрів, які відбивають істотні впливи й взаємодії змінних. Для розв’язання цієї задачі (перевірки відповідної гіпотези) використовується критерій .

Спочатку обчислюється різниця значень критеріїв , розрахованих відповідно для насиченої моделі к-го порядку й моделі, що відрізняється від насиченої моделі параметром, який перевіряється на значущість. Критерій, побудований у такий спосіб називається критерієм приватного зв'язку змінних. Критерій для маргінального зв'язку будуватися подібним чином лише з тією різницею, що його значення обчислюються за таблицею, знайденою підсумовуванням частот вихідної багатомірної таблиці спряженості за критеріями змін, що не входять у досліджуваний на значущість параметр. Число ступенів вільності для критеріїв частинного й маргінального зв'язку для групи змінних Z обчислюється за формулою :

(4.6)

де I, J, K – число рівнів ознак A, B, C відповідно, δ^ZA = 1, якщо А входить в Z, і а якщо ні, то δ^ZA = 0 і т. п.

Критерії частинного і маргінального зв'язків еквівалентні за λ параметрами, які представляють вплив окремо взятих змінних. Відбір параметрів проводитися за наступним правилом: а) якщо обидва критерії (частинного і маргінального зв'язку) показують значущість параметра, то він не виключається з початкової повної моделі; б) якщо обидва критерії вказують на його незначущість, то параметр виключається з моделі; в) якщо ж за одним з критеріїв параметр значущий, а за іншим - ні, то необхідно проводити спеціальне дослідження.

Висновки