Контрольная работа: Логарифмічно-лінійний аналіз

де f_ijk ,λ – невідомі параметри, які називаються:

λ_i ^A – ефект i-ого рівня ознаки А, i=1,..,I;

λ_j ^B - ефект j -ого рівня ознаки B, j=1,..,J;

λ_k ^C - ефект k-ого рівня ознаки C, k=1,..,K;

λ_ij ^AB – ефект взаємодії i-ого рівня ознаки А та j -ого рівня ознаки B;

λ_ik ^AC – ефект взаємодії i-ого рівня ознаки А та k-ого рівня ознаки C;

λ_jk ^BC - ефект взаємодії j -ого рівня ознаки B та k-ого рівня ознаки C;

λ_ijk ^ABC – ефект взаємодії i-ого рівня ознаки А, j -ого рівня ознаки B та k-ого рівня ознаки C;

f_ijk - гіпотетична частота в (i,j,k)-ій комірці

Оцінки параметрів знаходяться за методом максимальної правдоподібності й набувають вигляду:

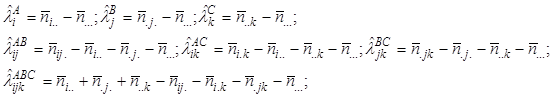
де

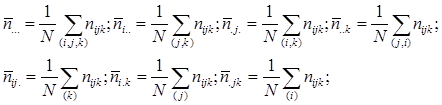
Для перевірки гіпотез

H₀ : λ_ij ^AB =0, i=1,..,I, j=1,..,J – про незалежність ознак А і В;

H₀ : λ_ik ^AC =0, i=1,..,I, k=1,..,K – гіпотеза про незалежність ознак А і C;

H₀ : λ_jk ^BC =0, j=1,..,J, k=1,..,K – гіпотеза про незалежність ознак B і C;

H₀ : λ_ijk ^ABC =0, i=1,..,I, j=1,..,J, k=1,..,K – гіпотеза про незалежність ознак A, B і C

використовують критерій та критерій частинного зв’язку ознак.

Критерій . Якщо гіпотезу Н₀ відхиляти при:

і не відхиляти в супротивному разі, то з імовірністю α гіпотеза відхиляється, коли вона справедлива. n – кількість всіх комірок, p - число оцінюваних очікуваних частот при умові незалежності змінних,

Критерій частинного зв’язку ознак . Якщо гіпотезу Н₀ про взаємозв’язок ознак А і В відхиляти при

і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Якщо гіпотезу Н₀ про взаємозв’язок ознак А і C відхиляти при