Контрольная работа: Математические методы и модели

Вывод: Согласно критерию Гурвица стратегия СЕ обеспечивает максимальное значение линейной комбинации

Критерий Сэвиджа

Чтобы оценить, насколько то или иное состояние природы влияет на исход в соответствии с критерием Сэвиджа вводится показатель риска(r ij), определяемый как разность между максимально возможным выигрышем при данном состоянии (Rj) и выигрышем при выбранной стратегии (Si)

; при ,

где rij - показатель риска;

bj - максимально возможный выигрыш;

x ij - выигрыш при выбранной стратегии

На этой основе строят матрицу рисков, которая показывает "сожаление между действительным выбором и наиболее благоприятным, если бы были известны намерения природы". Затем выбирается такая стратегия, при которой величина риска принимает минимальное значение в самой неблагоприятной ситуации

Без риска	С риском	Без риска	С риском	Без риска	С риском	Без риска	С риском	Без риска	С риском	Без риска	С риском	Max rij
1	2	3	4	5	6
А	100	90	120	30	130	20	130	40	120	30	110	40	90
Б	110	80	90	60	150	0	120	50	120	30	100	50	80
В	150	40	150	0	100	50	90	80	100	50	90	60	80
Г	130	70	100	50	110	40	120	50	120	30	110	40	70
Д	150	40	110	40	110	40	100	70	130	20	150	0	70
Е	190	0	90	60	100	50	170	0	120	30	90	40	60
Ж	100	90	140	10	140	10	140	50	130	20	100	50	90
З	120	70	150	0	130	20	130	40	120	30	90	60	70
И	140	50	120	30	130	20	120	50	150	0	100	50	50
мах	190	150	150	170	150	150

S = 50

Вывод: В соответствие с критерием рекомендуемая стратегия СИ, выбирая её в самом худшем случаи наше сожаление не превысит 50.д.ед.

2.2При заданном распределении состояний факторов внешней среды определить стандартные статистические показатели (среднюю ожидаемую прибыль, дисперсию, коэффициент вариации прибыли) и обосновать выбор стратегии по индивидуальному отношению к риску.

0,2	0,4	0,1	0,2	0,05	0,05
1	2	3	4	5	6
А	100	120	130	130	120	110
Б	110	90	150	120	120	100
В	150	150	100	90	100	90
Г	130	100	110	120	120	110
Д	150	110	110	100	130	150
Е	190	90	100	170	120	90
Ж	100	140	140	140	130	100
З	120	150	130	130	120	90
И	140	120	130	120	150	100

Вычислим среднюю ожидаемую прибыль по формуле:

МА=100*0,2+120*0,4+130*0,1+130*0,2+120*0,05+110*0,05=118,5

МБ=110*0,2+90*0,4+150*0,1+120*0,2+120*0,05+100*0,05=108

МВ=150*0,2+150*0,4+100*01+90*0,2+100*0,05+90*0,05=127,5

МГ=130*0,2+100*0,4+110*0,1+120*0,2+120*0,05+110*0,05=112,5

МД=150*0,2+110*0,4+110*0,1+100*0,2+100*0,05+150*0,05=119

МЕ=190*0,2+90*0,4+100*0,1+170*0,2+120*0,05+90*0,05=128,5

МЖ=100*0,2+140*0,4+140*0,1+140*0,2+130*0,05+100*0,05=129,5

МЗ=120*0,2+150*0,4+130*0,1+130*0,2+120*0,05+90*0,05=133,5

МИ=140*0,2+120*0,4+130*0,1+120*0,2+150*0,05+100*0,05=125,5

Вычислим среднее квадратичное (стандартное) отклонение:

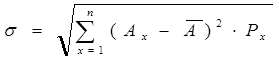
где s - стандартное отклонение;

Ax - результат для вероятности Px;

a - среднее ожидаемое значение результата;

Px - вероятность появления этого результата